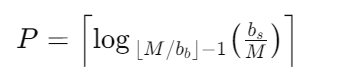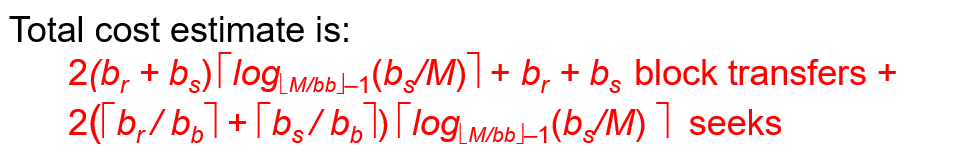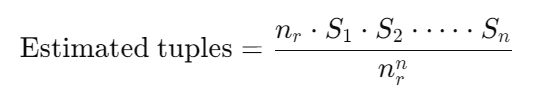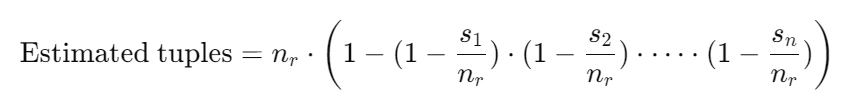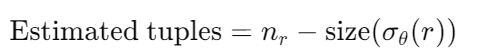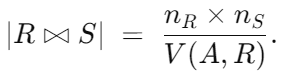有时间可以过一遍ppt
- 学长的笔记 Lec 14: Concurrency Control - NoughtQ的笔记本物理存储系统 - HobbitQia的笔记本
- 历年题 2017-2023.pdf
以下笔记前几章比较简单故较为省略
A4 纸
- 1.zip

Chapter 2: Introduction to Relational Model

实例

聚合函数：
- 表唯一： COUNT(DISTINCT 列)

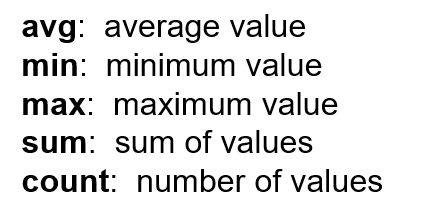
ANY 和 SOME 等效，与 ALL 区分

以下代码在自然连接后筛选

SELECT …
FROM A
NATURAL JOIN B
WHERE C;

要在之前就筛选的话

SELECT …
FROM (
     SELECT * 
     FROM A
     WHERE C1
     ) AS A_filtered
NATURAL JOIN B;

动态修改表的定义
- alter table r add A D
- alter table r drop A
insert into A(...) values(...); (可以忽略部分nullable的值)

嵌套子查询名字相同问题

外查询 不需要因为内查询里也有同名列就额外做限定
内查询 里如果要访问外层同名列，就必须用“外层别名.列名”来显式指明，否则 SQL 会默认先在内层自己找同名列；

Join问题

笛卡尔积，即 A,B ，需要 where来作筛选
natural join 是 join on 的最大交叉结果

Chapter 4: Intermediate SQL

隐式列名和显式列名，如果groupby 之后没有as 那么只能用显式列名重命名

插入视图，对于可更新视图，即如果满足“单表、无聚合、列直接一一对应”等条件的视图，才能把 INSERT/UPDATE/DELETE 映射到基表。
列补齐 default 还是 null 根据原有表定义

Chapter 5: Advanced SQL

trigger example

update 可以是 insert delete之类的

外键约束不可用：由于 time_slot_id 不是 time_slot 表的主（或候选）键, 应当用trigger来模仿外键references

(触发器风险：1. 触发器中出错导致关键事务失败 2. 级联执行风险，即无限递归 )

递归
rec_prereq(course_id, prereq_id)相当于临时创建了一个表; 每次递归rec_prereq 都增加行，增加的行就是原始的那些行(rec_prereq.course_id)(我们要查询这些行的所有pre) 和和它隔代的那些新行(prereq.prereq_id，在这里prereq一直起到一个提供信息的东西，它不更新)，

然后条件为rec_prereq.prereq_id = prereq.course_id

Chapter 7: Entity-Relationship Model

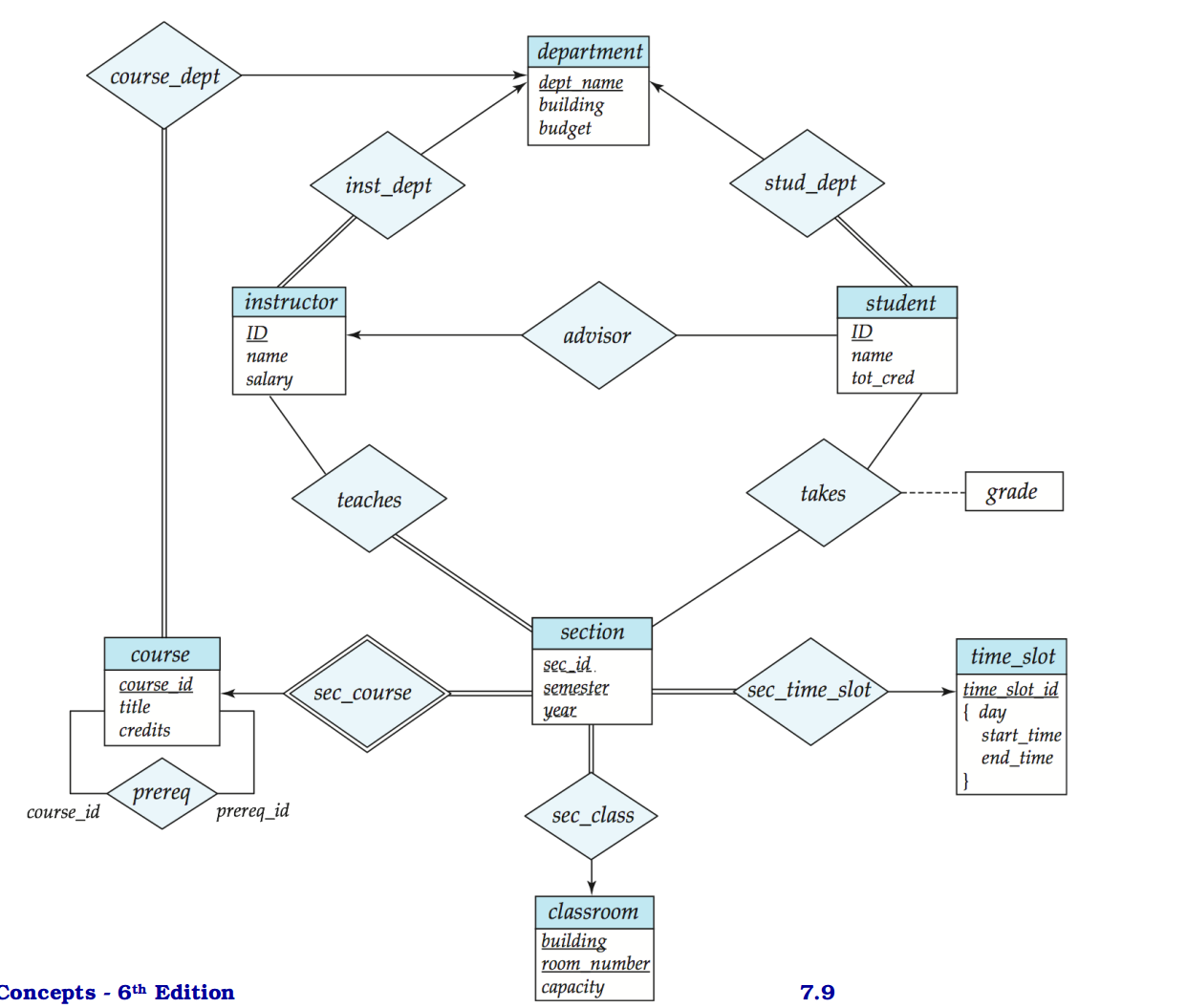
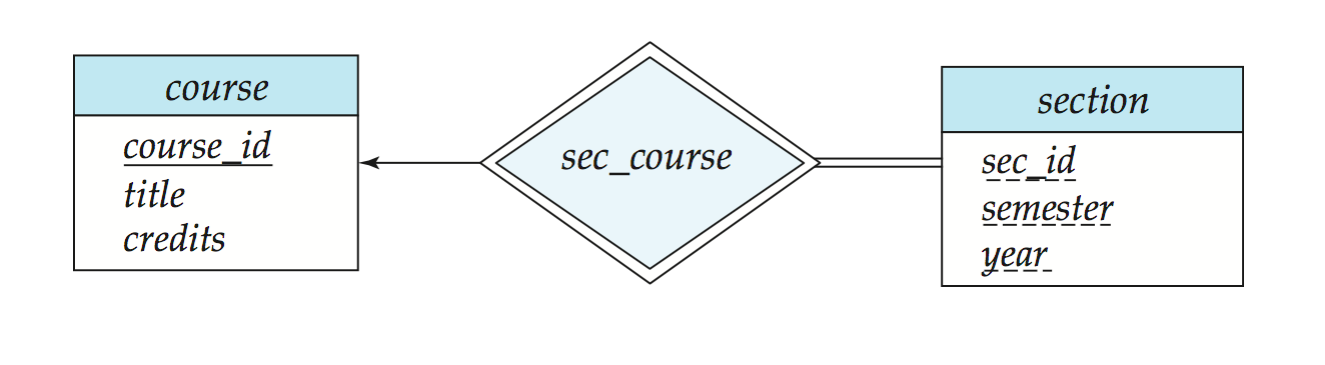
section 和 course 之间是弱实体关系
- 由于是弱实体，section必须要依赖且仅依赖一个course来distinguish itself,所以relationship是双线菱形的同时，也要加箭头和双线
- 如果把 course_id 显式放到 section 中，那么等价于把 section 当成一个强实体，原本的标识性联系 sec_course 就多余了

关系集的主键

一对一
- 通常两个实体的主键之一就足够唯一标识关系,但也可以两个都加
一对多
- “多”方的主键加上“1”方的外键通常就足够唯一
多对多
- 必须把双方主键全都串在一起，才不会出现重复的配对，也才是最常见的“交叉—关联表”

"一对多"的Redundancy

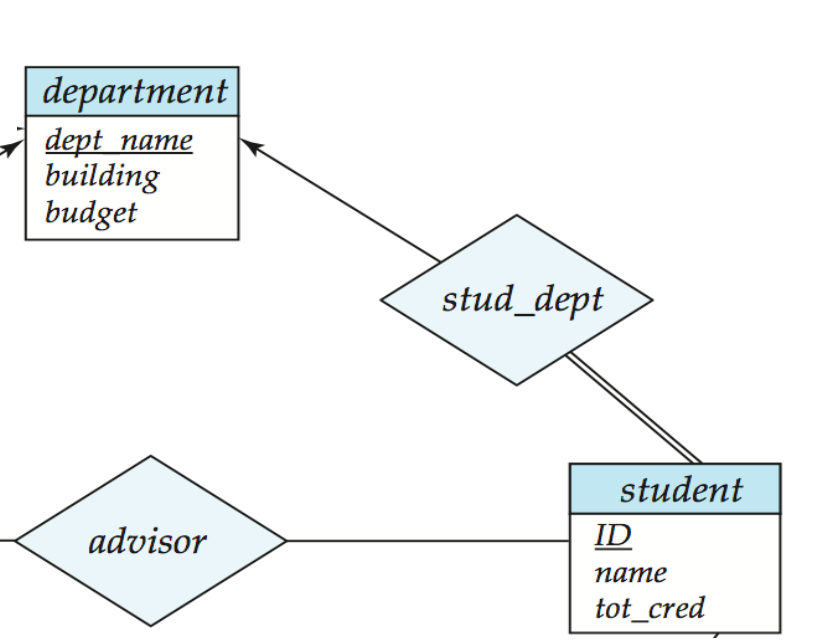
对于这样的关系，关系stud_dept实际上冗余了student.ID ，可以直接去掉此菱形，把dept_name 放在student entity内
- 当然，当这个多值（这里是department）的部分可以是空的话，去除关系要看是不是允许dept_name 在 student内允许为null

“关系”的升级

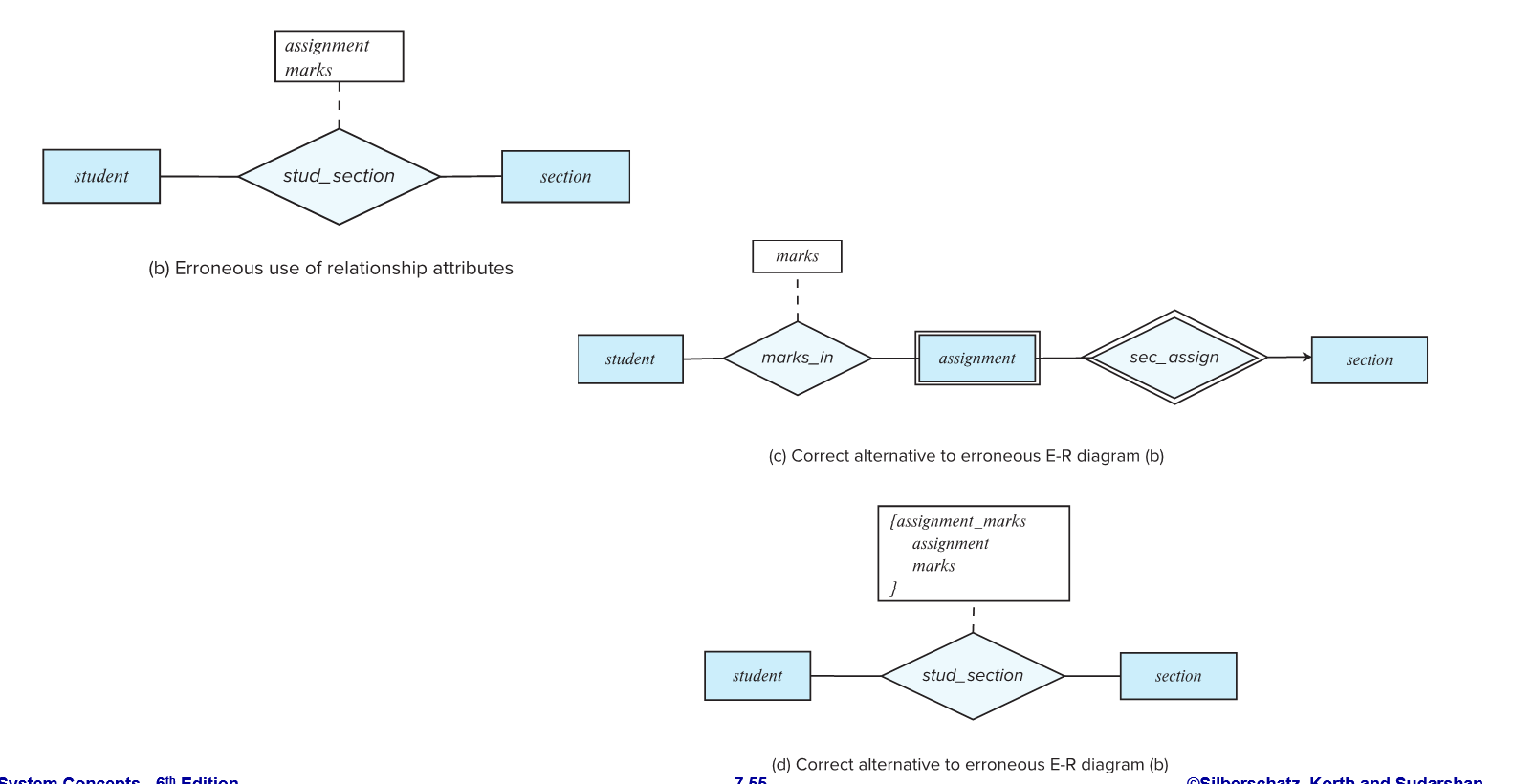
一般来说，关系的属性只能从连接的两个entities里取出，一旦要加上自己的独立的属性，就要虚线衍生出方块里面记录新属性

多元关系和二元关系

二元模型简洁，查询方便，理论上，你总能把任何 n-ary 关系，拆成多条二元关系，但有可能丢失原意，或者不够灵活
- 拆开后，就看不出来“这三个对象必须共同关联”，只剩下“AB 有关”、“BC 有关”“AC 有关”三件事。
- 也无法保证“要么三者都在，要么都不在”。
  - 解决方法1：用触发器，约束，但不够优雅
  - 方法2：把关系用弱实体替代，其主键为n个外键 (A_pk,B_pk,C_pk,......)

特化和泛化

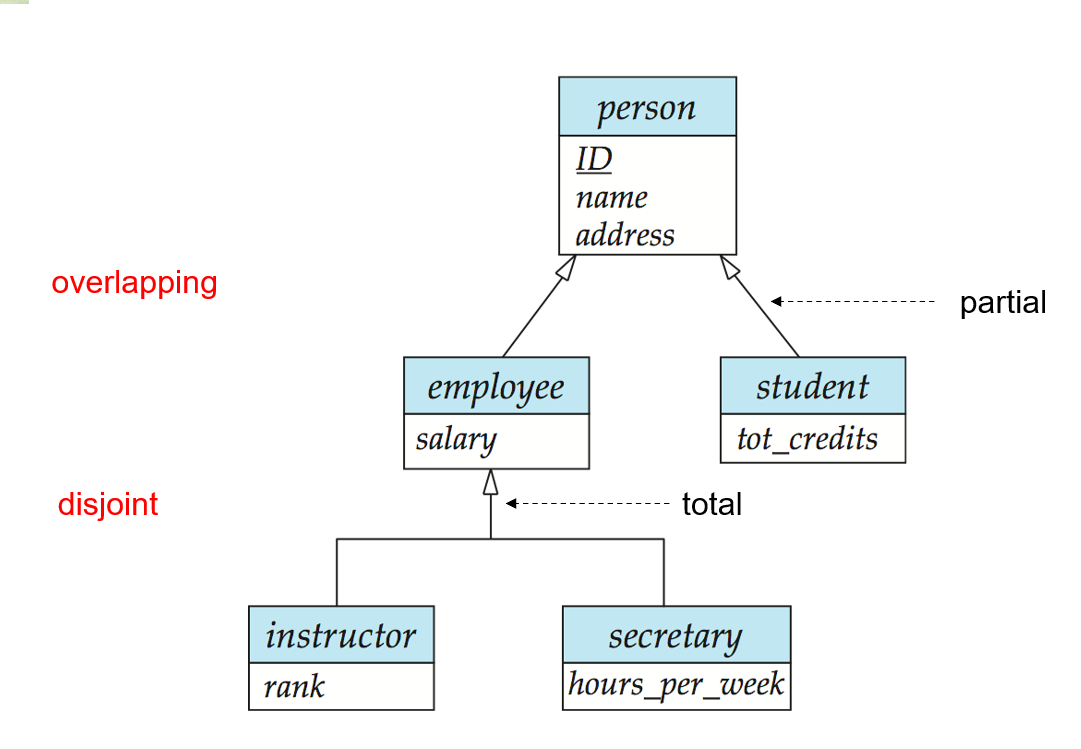
total 表示 employee只能是instructor或者secretary，partial表示可以只是person；用箭头加标注区分
overlapping表示既可以是employee又可以是student，用两根独立的线指向
- 有三种方法来表示

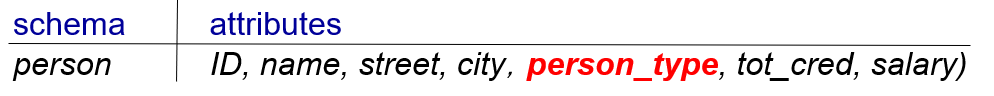
Chapter 8: Relational Database Design

无损分解

对拆分后的子表做自然连接，必须精确重建原表的所有行，且不多也不少。

有损：一个ID可能对应多个name
要做到无损分解，必须保证 公共列（JOIN 列）在至少一个子表中是候选键

第一范式

第一范式要求“每个属性值都是不可再分的原子单元”。
- 如果拆分 CS0012 来获取信息(0012)，就破坏了原子性

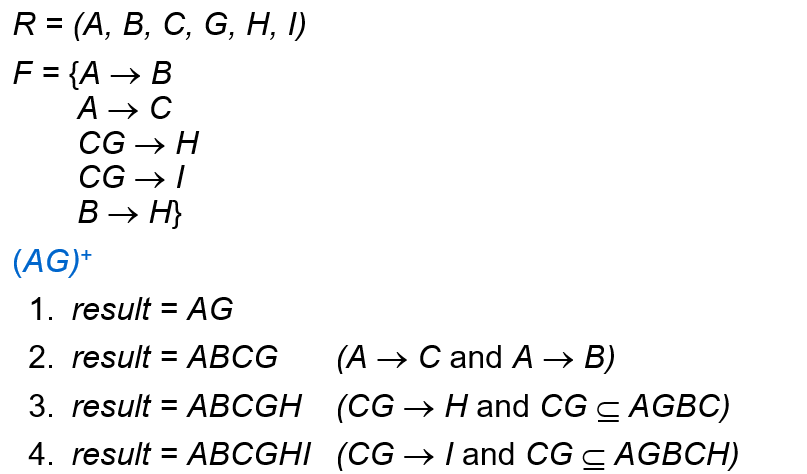
依赖闭包

给定一个关系模式 RRR 上的函数依赖集, 找出所有可以从 F 中 逻辑推导（imply）出来的依赖——包括已经写在 F 里的

Algorithm to find α⁺

找某一关系的闭包的话，先将每个单独元素的排列组合（共2ⁿ-1种）列出来，找到每一个的最大闭包，再找最大闭包的子集（2^m-1）个

Canonical Cover

重复以下步骤直至没有改变：
- replace α₁ -> β₁ and α₁ -> β₂ with α₁ -> β₁β₂
  - 删除冗余依赖
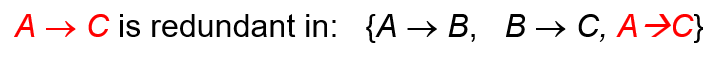
  - 右侧依赖冗余(给出了已有的结论)
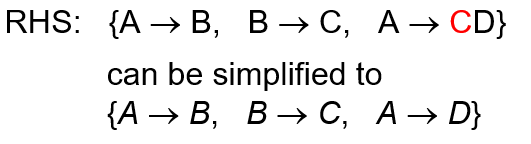
  - 左侧依赖冗余
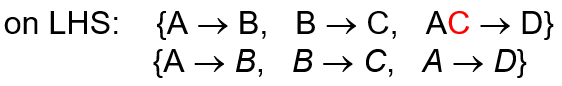
画图更加方便

BCNF

需要满足以下条件

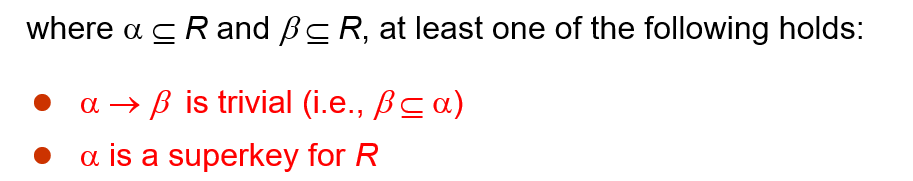
得到BCNF的方法

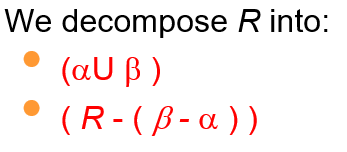
原关系是 {A->B , B->C }，拆成 {A->B},{A->C} 虽然无损连接，但是保持依赖被去除了（这样之后信息也没有被删除, 只是不体现保持依赖）
- 保持依赖必须要推出原关系，如果要恢复保持依赖自然连接{A->B}和{A->C}

BCNF分解可能会不保证保持依赖,如下：

这里意在把一个个关系拆开，在拆的过程中只关心 R（A,B,C,E）等，不关心R其中的元素的具体关系；所以我们能在下面这个答案中看到R（A,E）；因为A,E共同组成候选键，所以R（A,E,X）这种A E共存，且A指向其他元素的关系，A指向X必定会被分解

BCNF的好处：

一定程度上避免了数据冗余、更新异常、插入异常、删除异常

为什么呢？

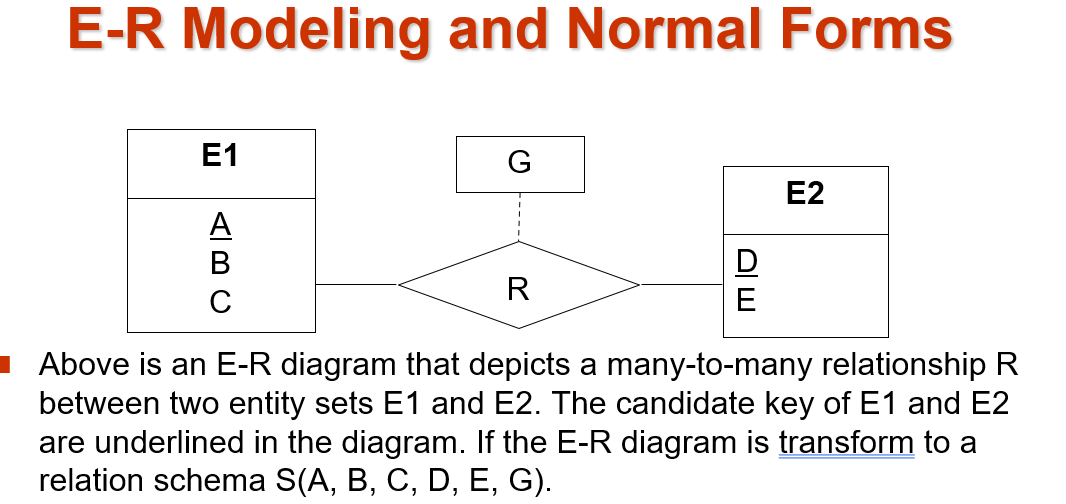如图的多对多关系，F1： R(ABCDEG) 可以被拆分为 F2 : R1(ABC) R2(DE) R3(ADG)

对于 F1 ，由于 A 不是候选键，而一旦插入一条 A ，就需要 AD 一起插入，来保证每一个行对应候选键的唯一性；而对于F2，如果插入A，因为A是候选键，所以不需要额外操作；

第三范式

不能完全杜绝“同一对属性多次重复写入”或“某些行里留空值”的情况。
但 3NF 总能保证依赖保持和无损连接

第三范式分解

数据库系统——3NF与BCNF模式分解 - Unalome - 博客园

求F的canonical cover，即去除冗余依赖，去除左侧冗余，右侧冗余
为每个依赖生成一个子模式（R1，R2，R3......）
确保有一个子模式包含候选键（例如有一个R(abdf),并且ad是候选键），如果没有的话单独加一个模式
（可选）去掉真子集的冗余模式（例如有R3={a,b,c}，R4={a,b},那么去除R4）

多值依赖

注意上方，只需要四个rows就行了，属性只需要划分出3种就行了
四个元组在α上是一样的，β 与 R-α-β 相互独立，且 t1与t3 t2与t4 在 β上一样， t1与t4 t2与t3在 R-α-β 上一样

任何依赖同时也是多值依赖（令t1=t3,t2=t4即可）

4NF

4NF 比 BCNF 还要严格

Denormalization

范式化好处：消除冗余、保证一致性、避免更新／插入／删除异常
范式化代价：为了完全消除冗余，会把信息切分到很多表里
查询时就常常要跨表做 JOIN，尤其在 OLAP、报表、仪表盘这些场景里，JOIN 太多就会非常慢

所以在某些“读多写少”、“对延迟敏感”的应用里，我们宁愿多存几份数据也要让查询少跑几个表、少做几个 JOIN。

Chapter 10: Storage and File Structure

存储record（freelist）

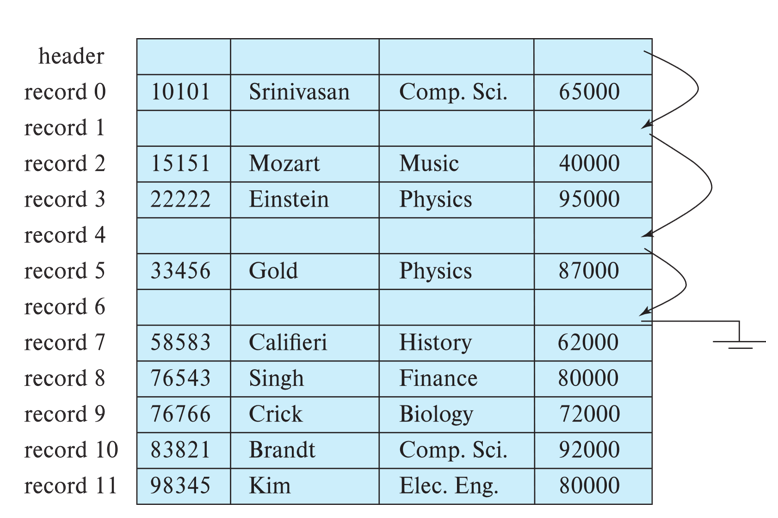
对于其中的一行，存储在“可变长度”字段，也就是minisql的bitmappage:

“可变长度”字段

左侧存储数据开始位置和长度，中间记录是否为null值，右侧为数据

Slotted Page Structure

管理以上的众多个“可变长度”字段，相当于minisql的disk_file_meta_page, 记录
- 记录条目数，表示当前页里有多少条记录
- 空闲空间结束位置，指示从页尾往回算，记录数据开始之前还剩多少连续的空闲字节
- 每条记录的“槽”条目 通常占 4–8 字节，里面记录对应记录的 起始偏移长度
插入新记录 : 记录区“顶端”（紧邻已有记录的上方）写入新记录
删除后要移动记录，保持记录之间无空白

接下来就是组织这些block的数据结构了，对应minisql 的 b+树，当然也可能是其他数据结构

Organization of Records in Files

Heap File Organization

具有特点：写入后基本不会移动，只要某页有空余就可以插入
- 问题：怎么知道哪里有空位
- 方法： Free-Space Map，维护一个数组，其中每个entry存放一个页，存放它的空闲信息；如果文件页很多，就再加一层; 这一层存放上一层对应entry列的最大的空闲等级

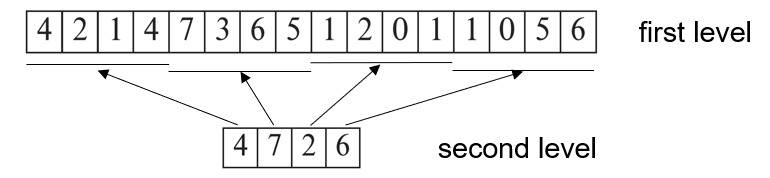
不是“强一致”刷写——允许有点儿旧数据；只要定期把 FSM 写回磁盘，并在插入／删除操作中发现不符，就去修正就行，

Sequential File Organization

顺序组织，按某个“搜索键”排序，在物理上是连续的

在有一个“搜索键”作索引，所以可以在O(logN)上查找到记录；但同时也有指针链来记录哪些地方有数据
- 删除时相应slot标记为空，链表跳过这一个记录
- 插入时，若有足够的 free space，则直接插入并更新指针链；若无空闲空间，则在溢出块中插入，并更新指针链
  - 随着多次插删，主文件中会堆积很多空洞，溢出块里会有大量跳转，需要定期重组

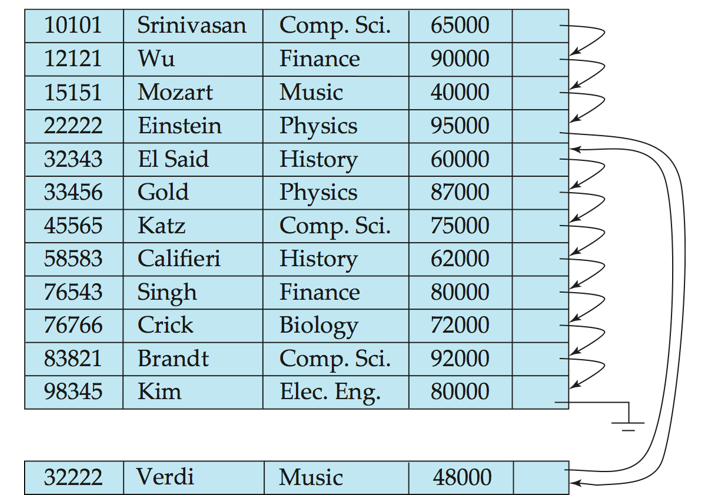
Multitable Clustering File Organization

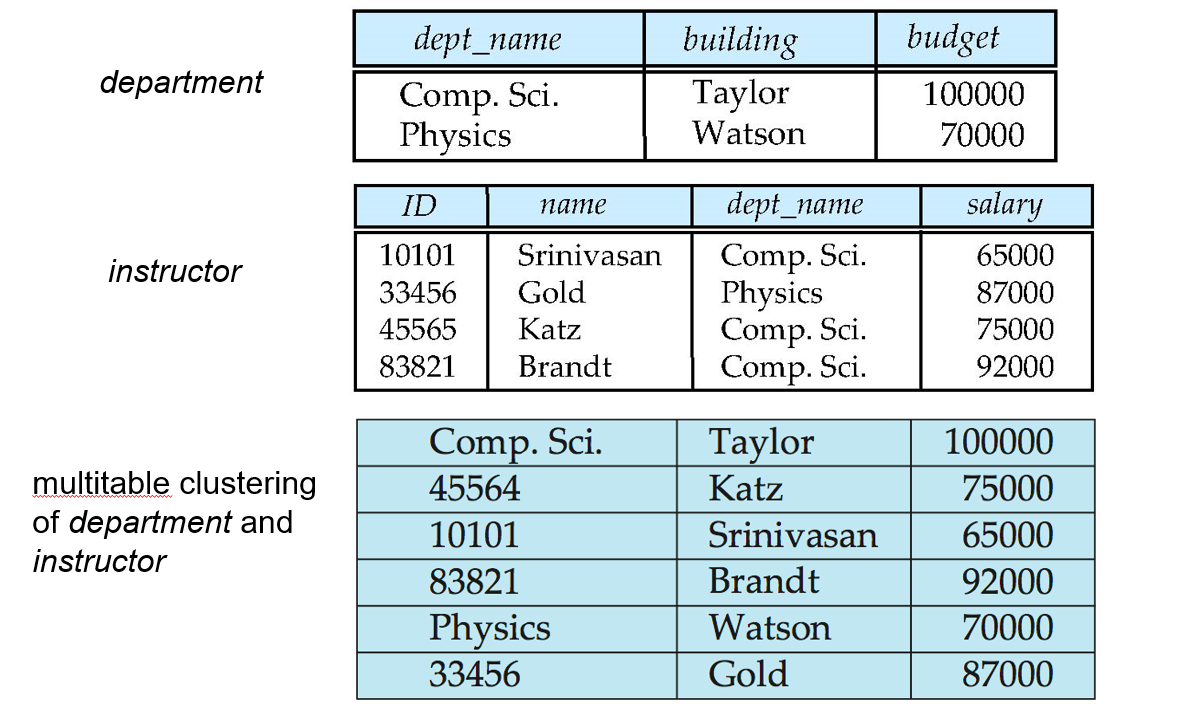
优点： Join 性能极好：department 与其 instructor 的数据物理上已经在一起，扫描一次就能拼出完整的结果
缺点：单独访问一个表的性能不佳
- 但可以通过一个链表来链接起来department

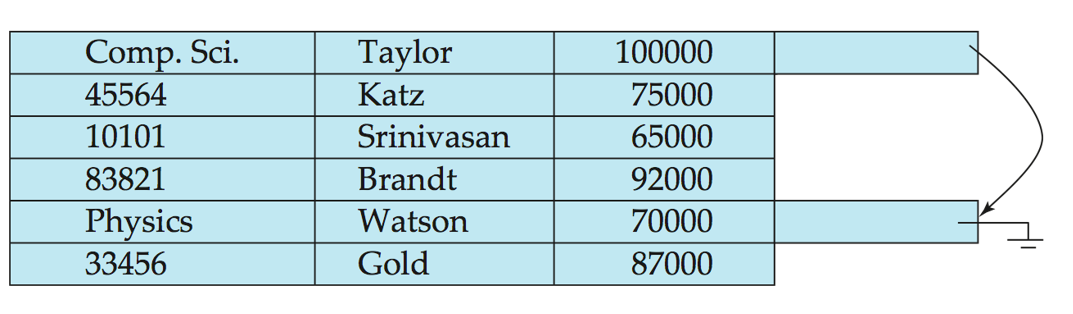
元数据Metadata也可以当作一串表来存储

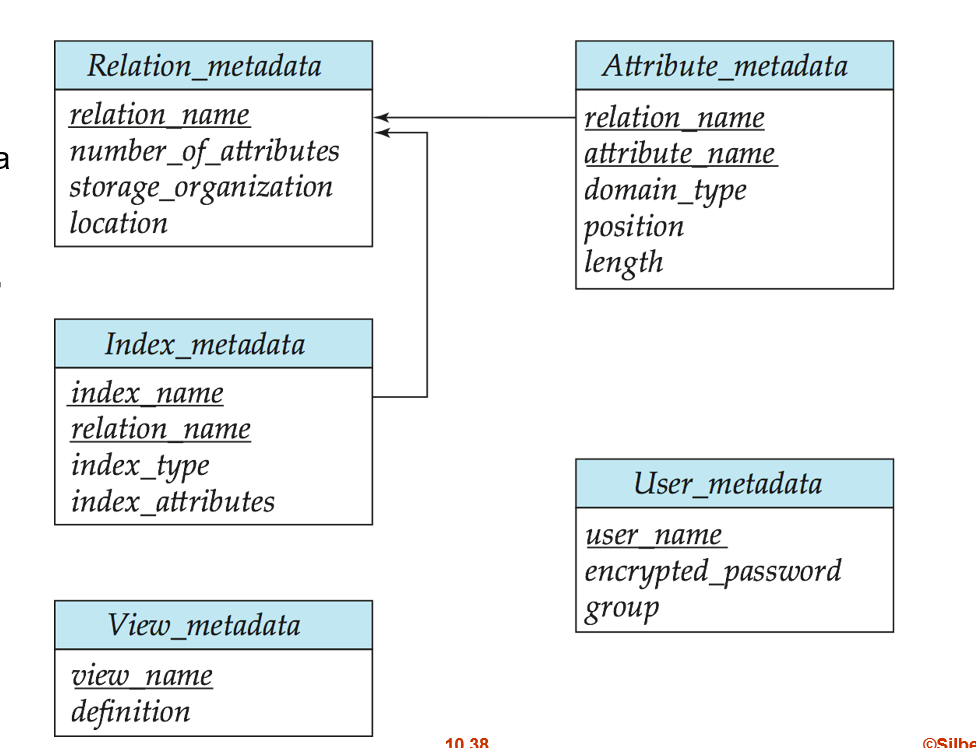
分别记录有哪些表及其基本信息，表的列，表的索引，视图，用户信息

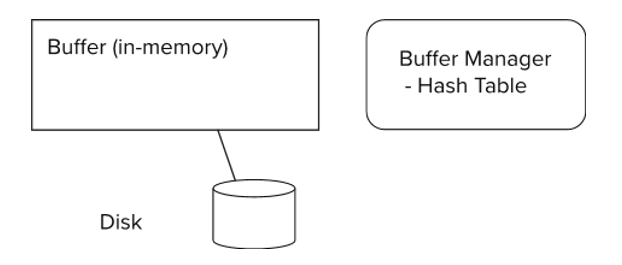
缓冲区管理

minisql 的 buffer_pool_manager

底层流程示例

读请求：用户事务要读某行数据→定位到对应的磁盘块号。
哈希查找：缓冲区管理器在哈希表中查 <文件, 块号> --> （映射到）缓冲帧指针：
- minisql的实现是满足一个 unordered_set 和 list ，list 是双向链表所以可以满足LRU的实现逻辑，然后unordered_set 的查找平均为O（1）（list是O(n)）所以用unordered_set 来查找最快
  - 命中
  - 未命中：脏数据写回，替换

Chapter 11: Indexing and Hashing

索引

用来加速对文件（或表）中记录的查找
索引本质上是一份“辅助文件”，记录了映射关系 检索健-->指针
两种基本索引:
- 有序索引（Ordered Index）: 索引条目按检索键的大小维持排序状态, 支持范围查询和顺序扫描（例如 B+ 树、顺序文件索引）。
- 哈希索引（Hash Index）: 根据检索键通过哈希函数分配到若干“桶（bucket）”中。适合精确匹配（等值查询），但不支持范围查询。

有序索引

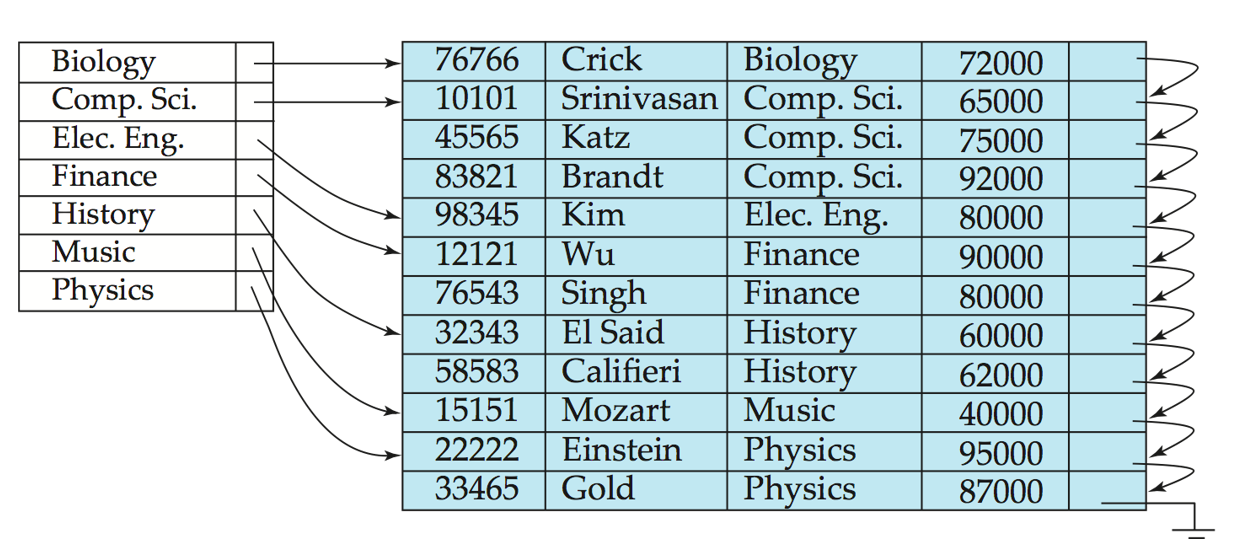
主索引（Primary Index／聚集索引）: 指定了底层文件中记录的物理存储顺序 , 但不一定是主键 对应概念索引顺序文件
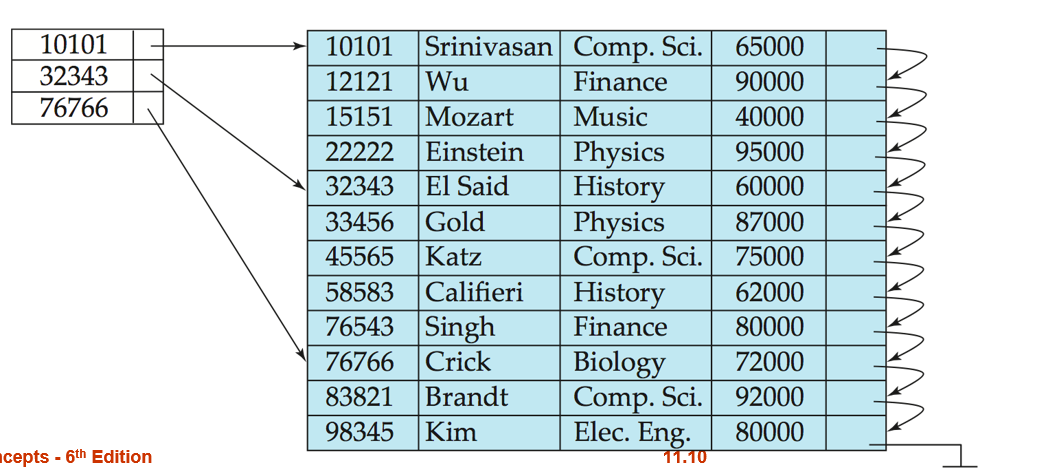
辅助索引（Secondary Index／非聚集索引）: 与文件物理顺序无关
classification
- 稠密索引：索引都包含条目相对于列的所有种类，
- 稀疏索引：索引不包含部分条目的相应列种类 (空间开销小，维护代价低，查询速度略慢：折中：每个block一个索引 (这里好像只能指主索引) )

多级索引

当主索引（Primary Index）太大，无法全部常驻内存时，直接查找依然要做大量磁盘 I/O，性能受限。
把主索引当作一个顺序文件，在其之上再建立一个“稀疏索引”——称作外层索引（Outer Index）指向内层索引的某个块

B+-Tree Index

Inner node ⌈n/2⌉ 到 n 个孩子(不是key)
Leaf node ⌈(n-1)/2⌉ 到 ⌈n-1⌉ 个孩子 (由于⌈(n-1)/2⌉ 是后向上取整的，所以可能看起来可能不会到一半)
If the root is not a leaf : at least 2 children.
If the root is a leaf : between 0 and (n–1) values.

the height of the tree is no more than ⌈log_⌈n/2⌉(K)⌉

插入的时候不会借节点(只会一直向上分裂)，只有删除的时候才会合并或局部重分配

合并（Merge）或重分配（Redistribute）

合并：若该节点与某兄弟节点（左右任一侧）合并后，其总键数 ≤ n，则执行“合并” ，父亲节点删除相应键值对，向上递归删除
重分配：否则执行重分配，父亲节点修改键，不递归

最坏情况下 insert/delete cost=O(log⌈n/2⌉(K)) ，即树高

练习题，计算每一层最小最大扇出记录个数
- 这里 (4096-4)/(18+4) + 1 的 +1 表示一个单独的value也算一个键值对计数，当然minisql不是这么实现的
- pid char(18)当作主键，所以算在索引长度内，在非叶子节点中都会出现它的身影

区分 B+ 树索引和 B+树文件组织

B+ 树索引	B⁺-树文件组织
“非聚集索引”/“辅助索引”	“聚集索引”/“索引顺序文件”
叶节点只存 <键, 指针>	叶节点本身就是数据文件

主索引，二级索引问题

按照主索引，二级索引等等其他索引建立的数个树的叶子节点一般都指向某个磁盘页+偏移，但一旦这些物理偏移改变了，所有树都要修改一次
- 因此，不存物理指针，改为在二级索引里只存 主索引的搜索键，使得 物理偏移改变时候，只需要主索引的叶子节点改变一次

一些优化

当键值对的长度可变的时候，改用空间利用率（node space utilization）作为分裂判据
前缀压缩
- 内部节点只保留能够唯一区分左右子树的最短前缀即可
- 叶节点多个相邻键有共同前缀写一次就行

B+树填充率

如果随机插入， 2/3 的叶子节点空间被填充，按索引顺序插入 (Bulk Loading)，1/2的空间被填充
- 如果对所有条目按键值排序，打包好每个叶子节点，自底向上，那么几乎所有都能被填充干净

多键（复合）索引

select ID from instructor where dept_name = “Finance” and  salary = 80000

使用多个 key当索引
- 最优场景：全等匹配；前缀等值+后缀范围
- 较差：前缀范围+后缀等值

Chapter 12: Query Processing

SQL 查询:

解析与翻译（Parsing & Translation） --> 查询优化（Optimization）-->计划执行（Evaluation）

查询代价估算中棘手的问题：

未知实际执行时到底能分配到多少内存，因此优化器通常采用“最坏情形估计”
不知道一开始缓冲池中的会不会被命中，因此默认所有 I/O 都是冷启动

Selection Operation

A1 : linear search

就是数据块依次读入内存
- worst cost = b_r * t_T + t_{S （其中br为存放块记录的数据块总数，tT是数据块传输时间）}
  - t_S只有一次是因为只需要寻导到第一个块的时间就行了，后面只需要顺序读而不需要寻导
- average cost = (b_r /2) t_T + t_S

A2 : (primary B+-tree index , equality on key)

固定代价： Cost = (h_i + 1) * (t_T + t_S)
- 由于内部节点较少，往往常驻内存，所以实际IO可能更小

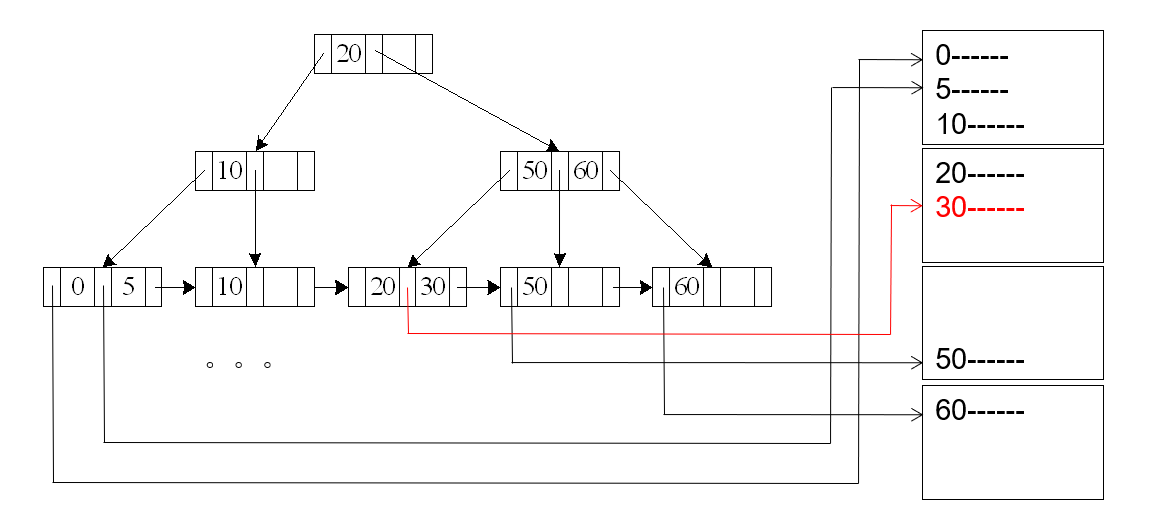
A3 (primary B+-tree index, equality on nonkey) [区分primary index 和 primary key！！]

当你的聚集索引（主索引）的搜索键并不是表的主键，而在该键上做等值查询时，可能会匹配多条记录
- 因此还要 叶节点链扫描
Cost = h_i(t_T+ t_S) + t_S+ t_T b

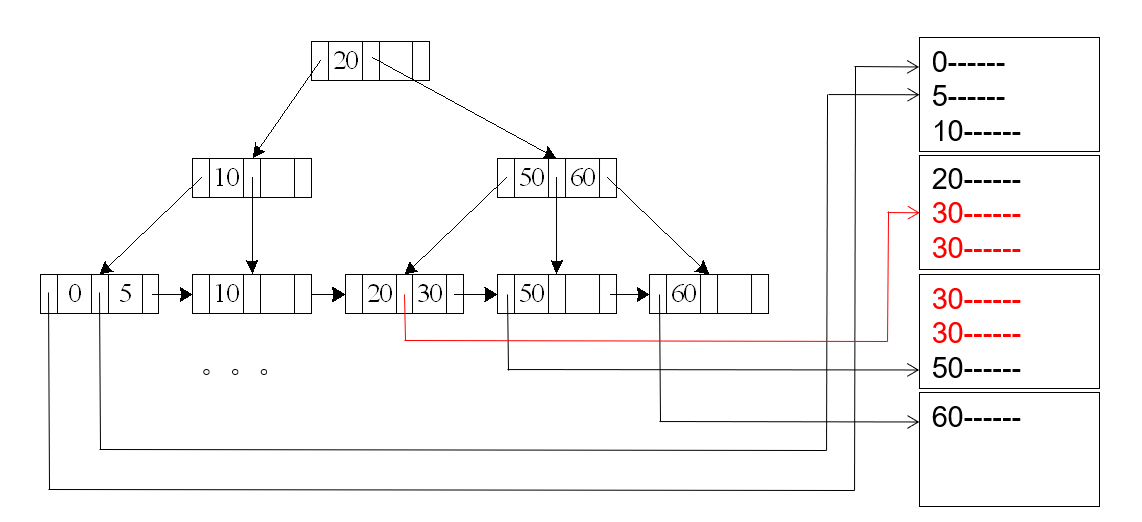
A4 (secondary B+-tree index , equality on key) [这里就不是聚集索引了]

这里和A2比较相似，只是最后的叶子节点存放的对应物理地址的顺序和叶子节点的顺序不是一致的，但无碍
- Cost = (h_i + 1) * (t_T + t_S)
- （当然，之前有个优化是把叶子节点指向聚集索引的叶子节点，这样的话cost就是 (h_i + 2) * (t_T + t_S)了）

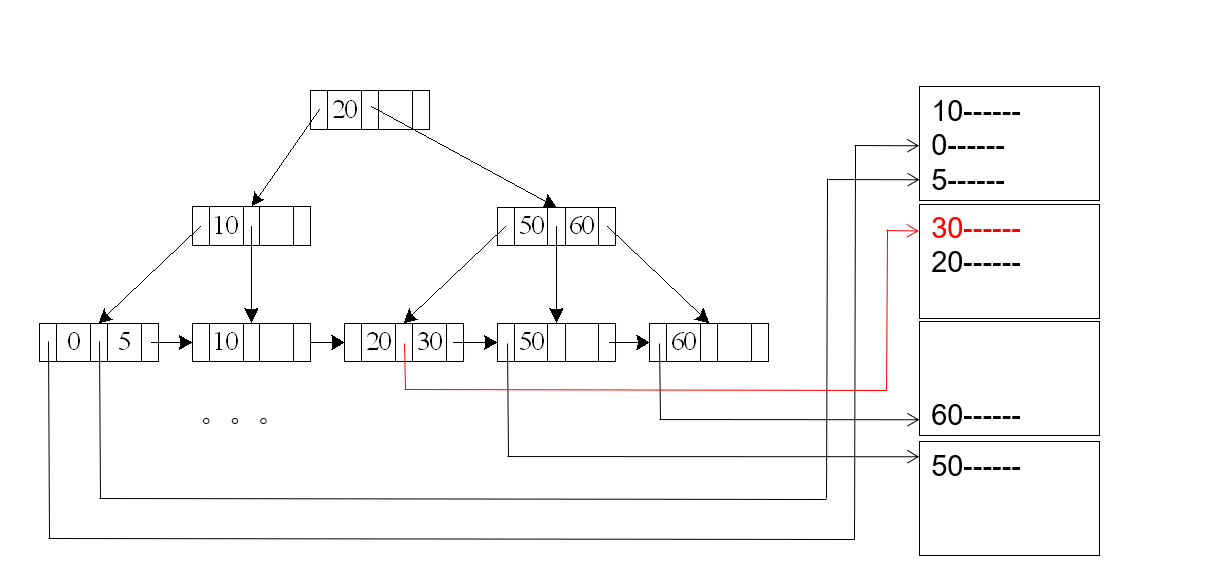
A4’ (secondary B+-index on nonkey, equality)

匹配多条记录
这里和 A3区别最大的地方在于，由于匹配的多条记录的物理地址可能分布在不同块（假设有n个不同块），所以对应的叶子节点也需要多个指针来指向这些块；因此，叶子节点的这些多个指针也可能会被分配到不同块里面（假设为m）【代价比较昂贵】
- Cost = (h_i + m+ n) * (t_T + t_S)

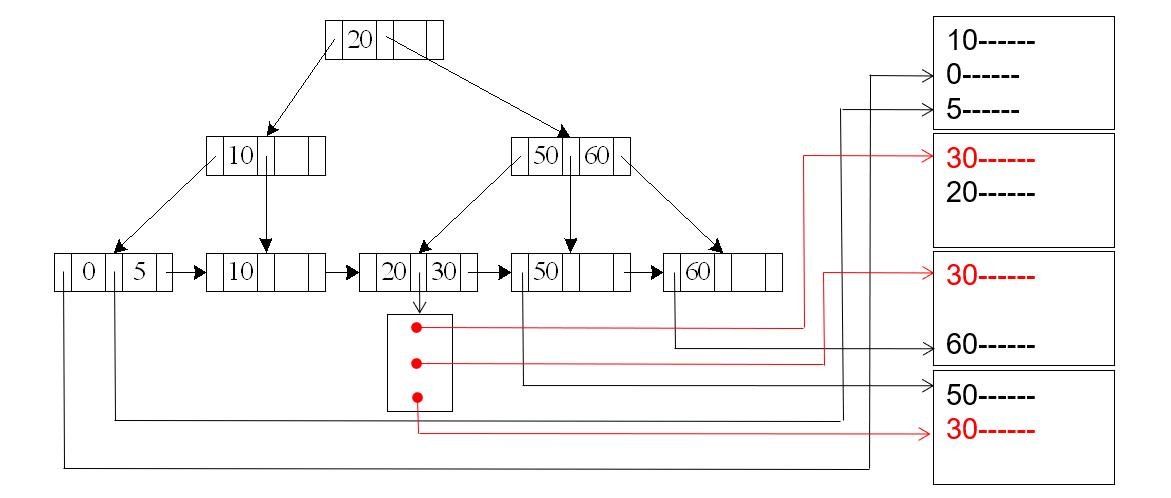
排序的三种常见策略

基于索引的排序
- 可先在待排序的关系上建一个索引（B⁺-树、聚簇索引等）
- 缺点：每次定位下一条可能都要一次随机 I/O（一个元组一块）
内存排序
- 当整个关系能一次性载入内存时，直接用快速排序（quicksort）或归并排序即可，
- 时间复杂度 O(Nlog⁡N)，不涉及磁盘 I/O
外部归并排序
- 分段 , 多路归并
- 既保证了 O(Nlog⁡N) 的排序性能，又最大程度减少磁盘 I/O

External Sort-Merge

1. Create sorted runs(归并段 )

设可用内存能容纳 M 个页（blocks），待排序的关系有 B 个页 ; 每次从磁盘顺序读入 M 页到内存, 在内存中对这 M 页记录进行任意内存排序; 一共会产生 N=⌈B/M⌉ 个已排序段(run);注意，一个run一般有多个block 。

2. Merge the runs (N-way merge).

① IF N < M
- 内存的N 个 blocks当作输入，1个block当作输出，读取之前N个run的第一个block
- repeat：不断读取N个中最小的元素并输出，读取输出一次之后删除这个run的第一个元素；如果这个run在内存中的block删除完了，那么把这个run在硬盘中的下一个block取过来
②N >= M
- 一次merge之后还不足以完全排序好，只是利用内存的 M-1 块形成更大的run
- 每做一轮，runs 数量会减少为原来的⌈1/(M–1)⌉；每个新 run 的长度都会扩大 (M–1) 倍；

3. 传输开销

归并轮数： P = ⌈log_M-1 (b_r/M)⌉
每次merge涉及到磁盘的读写，IO为2b_r, 最后一次merge只涉及到磁盘的读；总共block transfer为：2b_r⌈log_M-1 (b_r/M)⌉ + b_r（当对应到上述情况①的时候就是3*br (即 2b + b ，一次create sorted runs 和一次IF N<M)）
可以注意到，⌈log_M-1 (b_r/M)⌉ 实际上就是步骤2 的次数

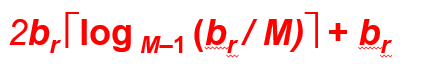
4. 寻道开销

初始跑阶段，寻道次数 = 2 · ⌈b_r / M⌉ （读和写各占一半）
- 虽然物理上这些块是连续存储的，但，寻道位置是不连续的；假如从位置A开始读，然后读到B（一共M块将内存填满），内存完成A-B这块区域的排序，然后还得寻道到A来写入，最后寻道到B开始下一轮读
而后面的merge的话，寻道次数与块为单位计算，合为 2*⌈b_r/M⌉ + b_r(2⌈log_M-1 (b_r/M)⌉-1)
- 为什么第一次是 ⌈b_r/M⌉ 而后面每一次merge 是 2b_{r ：}
  - 因为后面的归并的读入都是对于不同的run分别读入一块（block），不连续；然后写的话也是一块块写出去的，并且写出去一块之后紧接着往往是读，这里计算最差情况就是没有连续的情况

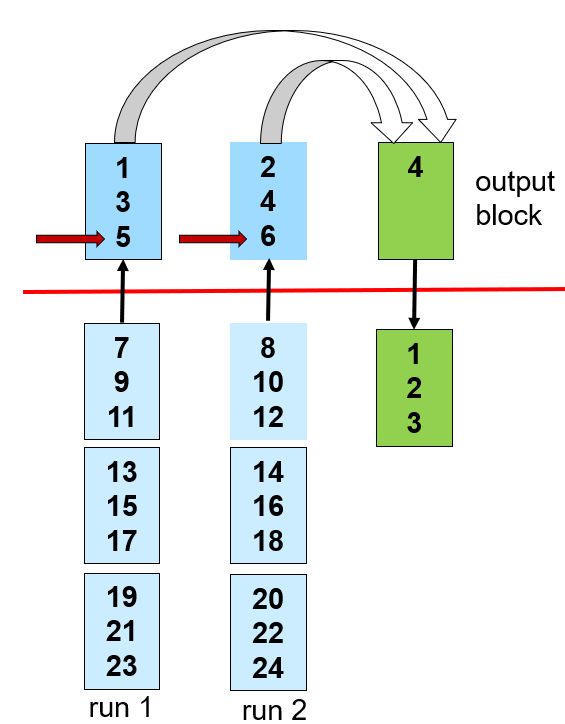
5. 避免多次寻道

给每个 run 分配多个缓冲块来显著减少寻道次数, 以归并论述和传输开销的增加为代价

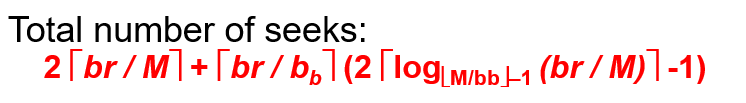
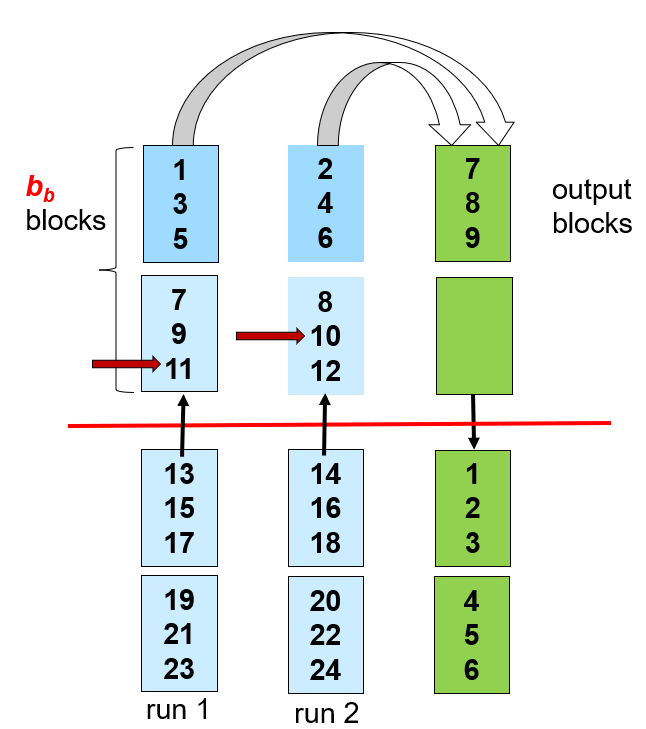
Join Operation

Nested‐Loop Join

读入的时候是先读1个r block，假设这个r block有n个tuple，则循环读n次s blocks；每一次循环读那些s block，都会与r block中的一个元组进行自然连接
最坏情况下（nᵣ 是 r 的元组数）
- I/O 代价（块传输）≈ nᵣ×bₛ + bᵣ
- 寻道次数≈ nᵣ + bᵣ
若较小的关系可装入内存
- 将其作为“内层”关系
  - I/O 代价仅 bᵣ + bₛ
  - 寻道次数仅 2 次

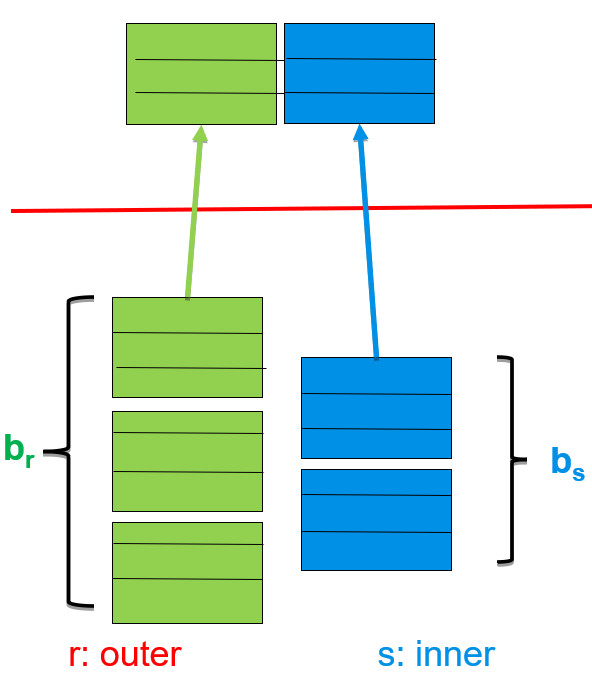
Block Nested-Loop Join（可以非等值连接，如大于，不等于之类的）

for each block Bᵣ of r do  
  for each block Bₛ of s do  
    for each tuple tᵣ in Bᵣ do  
      for each tuple tₛ in Bₛ do  
        if (tᵣ, tₛ) 满足连接条件 θ  
          输出 tᵣ⋈tₛ

最坏情况
- 块传输≈ bᵣ×bₛ + bᵣ
- 寻道≈ 2×bᵣ
最好情况
- 块传输≈ bᵣ + bₛ
- 寻道 = 2
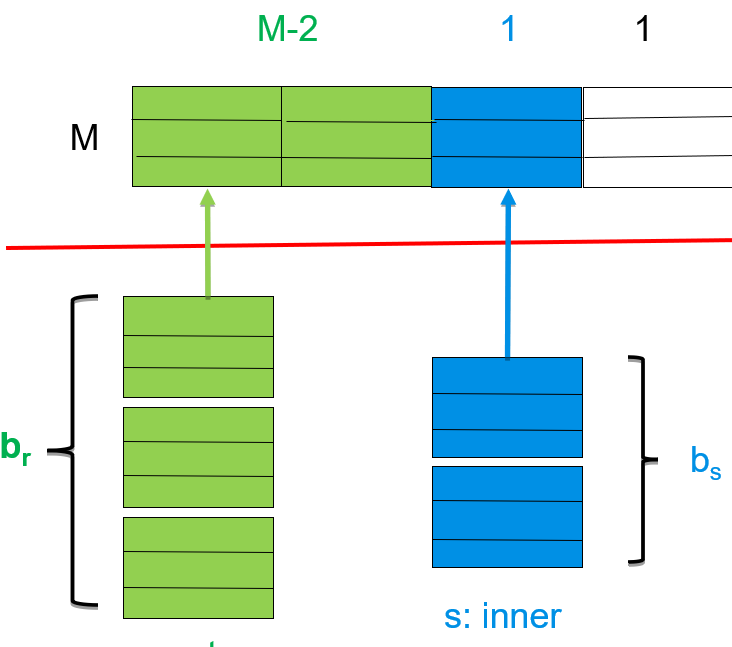
改进的块嵌套循环连接
- 在总共 M 个缓冲区页中，留出 M–2 页一次性缓存外关系 r 的多块，
- 剩下的 1 页用于缓存内关系 s 的当前块，另 1 页用于输出。
  - 块传输代价：⌈b_r/M−2⌉×b_s+b_r
  - 寻道次数： 2*⌈b_r/M−2⌉

Indexed Nested-Loop Join (仅适用于等值连接)

何时用索引替代全表扫描
- 仅限于等值连接 ; 且在内关系 s 的连接属性上已有可用索引
对每个 tᵣ ，借助 s 上的索引直接定位所有满足连接条件 θ 的 tₛ，并输出匹配对。

Merge-Join(仅适用于等值连接)

要求对连接属性上的两个关系 r、s 均已按该属性排好序；否则需先做外部排序。
给一个输入b_b 块的内存空间，做merge join，成本：
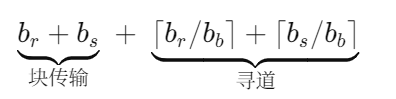
- 如果要排序，还得加上这部分的成本
- 归并连接要想在一次顺序扫描里完成，就必须保证“对于每个相同的键值，左右两边所有的元组都能装进缓冲区”。一旦某个键对应的元组组太大，可能在这部分上要降级到嵌套循环
在大小为 M 页的缓冲区中，如何在外关系 r（大小 bᵣ 页）和内关系 s（大小 bₛ 页）之间分配 xᵣ 和 xₛ 页（满足 xᵣ+xₛ= M），以使得归并连接的 I/O + 寻道（seek）总成本最小？

Hash-Join(仅适用于等值连接)

Hash-Join过程
- 1. 外部分区：把 R 和 S先用哈希函数 h 按属性 a 划分成多对小分区 (R₀,S₀), (R₁,S₁),…使得每对分区 S_i 都能「整块」装进内存(Ri没必要)。
  - i=h(a) mod (n+1)
- 2. 内存构建+探测：在内存里为 S_i 建二级哈希表（这次的哈希函数和第一步的不同，不然将会被分到哈希表的同一个index上），用 R_i 的每条元组去探测
  - 假设r 和 s 在属性a上join；相当于，只要 s 中每个元素的a值相同，就会用把a哈希归到这个哈希表的某个index上，用链表把这些元素串起来(每个index对应一个链表)，在这个链表上的所有元素的a值有可能不同，但r只需要线性扫描就可以把相同的选出来
N就相当于第一次hash的桶的个数，

递归分区

为什么n>=M 就要递归分区啊, 递归终止条件
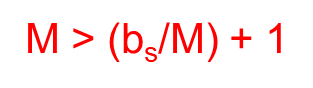
- 原因在于第一步（外部分区），n代表桶的个数，由于第一次哈希是n个桶一齐进行的，每个桶都应该有个内存页来将哈希后的结果写到磁盘中（一旦这个桶对应的内存页满了），然后读入也需要一个桶
过程
- 第一级分区：用哈希函数 h1 仅分成 M−1 路
- 第二级分区：对这 M−1个子分区，再用另一个哈希函数 h2 进一步分，直到子分区数小于等于可用内存页数。
- 何时不必递归
  - 只要 M>n_h+1，即 M>⌈b_s/M⌉+1，就能一次性把所有分区都缓冲，免去递归。

Cost of Hash-Join (无递归)

前提提示：没有递归，并且为了减少seek 采用了连续读 b_b 块（相当于那个读入缓冲块，变成了b个读入缓冲块）

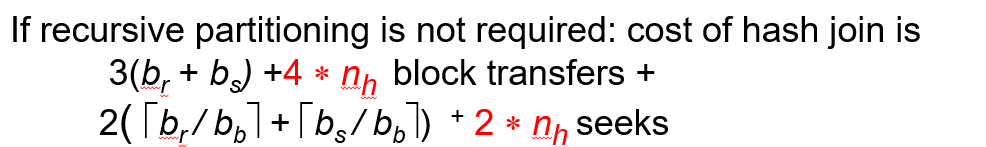
传输：外部分区，从磁盘传入算一次 b_r + b_s ，分区好之后写回磁盘算一次 b_r+ b_s，这时候由于部分分区有剩余的元素不满一个block还留在内存，也得写回磁盘两个表(r和s)各算一次 n_h （2n_h）（这里去最坏情况每个桶都有剩余），最后进行内存构建哈希表算一次 b_r+ b_s + 2n_h
seek：分区过程传入各需要 ⌈bᵣ/b_b⌉ + ⌈bₛ/b_b⌉ 次seek ①，忽略；写回磁盘是磁盘指针顺序不一定，共需要 (⌈bᵣ/b_b⌉ + ⌈bₛ/b_b⌉+2n_h)次 ; 最后内存构建和探测由于是顺序的所以忽略
- 选取Bb的时候注意输出快也要是Bb大小
- ①

Cost of Hash-Join (递归)

递归次数：

算子树的两种策略

物化：把每个算子（操作）生成的中间结果全部写到磁盘（或临时文件）里，然后下一个算子再从磁盘把它读出来当作输入。
- 算子之间完全解耦，调试和故障恢复都简单；中间结果可以复用
- 产生大量读写 I/O
流水线：不把中间结果写盘，而是把一个算子产生的每一条“活的”元组（tuple）立刻传递给下游算子，双方并行执行。
- 避免了中间结果的磁盘 I/O
- 内存管理更麻烦，需要在各算子之间协调缓冲区；算子间高度耦合，调度更复杂

Chapter 13: Query Optimization

选择操作要尽早做，然后再join

成本估算中所需的统计信息

n_r: 关系 r 中的元组数; b_r:存储 r 的元组的磁盘块数。 l_r: 每个元组的大小。 f_r: r 的 封装因子，即一个磁盘块能够容纳的 r 元组的数量。
V(A, r): 关系 r 中属性 A 的不同值的数量。这也等同于属性 A 在 r 中的基数。

选择操作（Selection）的大小估算方法

σA=𝑣(r): 选择操作在属性 A 上筛选值为 𝑣 的元组。
- nᵣ / V(A, r): 表示满足选择条件的记录数量估算值。
- 当选择条件为属性的键（key）时：此时，估算值为 1
当选择条件为属性小于或等于某个值 (σA≤𝑣(r)) 时
- 如果 min(A, r) 和 max(A, r) （分别是属性 A 的最小值和最大值）可用，则可以通过以下公式计算估算值：

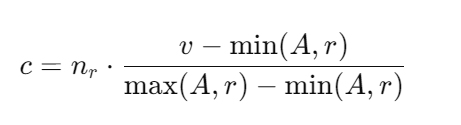
选择率（Selectivity）

对于一个条件 θᵢ，选择率是给定关系 r 中满足该条件的元组数与总元组数的比值。
连接（Conjunction）(如果各元素相互独立)
析取（Disjunction）
否定（Negation）

Join操作的大小估算方法

If R∩S is a key for R, then a tuple of s will join with at most one tuple from r.
Therefore, (the number of tuples in r⋈s) ≤n_s.

If R∩S in S is a foreign key in S referencing R, then the number of tuples in r⋈s= the number of tuples in s.
- 相当于s中的foreign key没有r中没有的元素，保证了join后不会删去
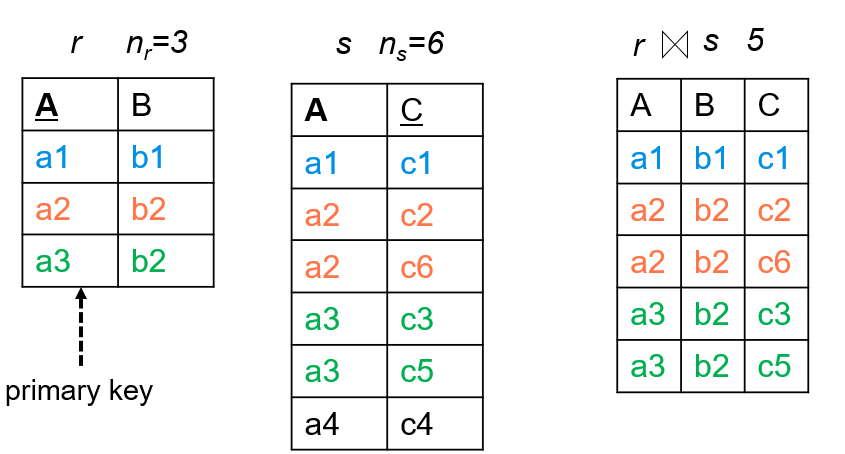
其他情况下：
- 如果我们假设属性 A 在 S 中有 V(A,S) 个不同取值，且每个 R 中的元组都能“匹配到”同一个 A 值的 S 中某些元组，则
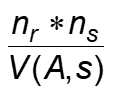
  - 这里的除以 V(A,S) 实际上有两个功能；因为R中的每个元组都能匹配到S中的某些元组，所以S的元组种类肯定会比R多；如果R的元组种类有无穷多个，那么匹配出来的大小为0；这和除以V(A,s) 相符，和除以 V（A，r）不符；所以选择前者
- 反之：
- 取二者中较小的一个，通常能得到更稳健的估计。
  - 取两者的最小值是因为不知道两者是否是某个总能匹配另一个，所以选择保守的估计;
eg.

其他运算符大小估算

聚合和投影的估算为 V(A,r)
左外连接为 r⋈s + sizeof ( r )
双外连接为 r⋈s + sizeof ( r ) + sizeof ( s )
Joins: r⋈s, estimate V(A, r⋈s)
- If all attributes in A are from r, the estimated
  - V(A, r⋈s) = min ( V(A,r) , n _r⋈s)
For min(A) and max(A)
- be estimated as min(V(A,r), V(G,r))

Choice of Evaluation Plans

局部与全局

归并连接（merge-join）：虽然可能比哈希连接成本高，但它能提供一个排序的输出，这可以减少外部层次聚合（outer level aggregation）的成本。
嵌套循环连接（nested-loop join）：可能为流水线处理提供机会，从而减少整体成本。

查询优化器的实际策略

成本驱动的优化（Cost-based approach）：搜索所有可能的查询计划并根据成本选择最优的计划。
启发式优化（Heuristic-based approach）：使用启发式方法来选择查询计划。

优化嵌套子查询

这里每一行都要查询调用

select ...
from L1
where P1 and exists (
    select *
    from L2
    where P2
)

可被替换为(创造临时表，这样就可以作merge join ， hash join 了)

create table t1 as
select distinct V
from L2
where P2¹

select ...
from L1, t1
where P1 and P2²

万圣节问题

当你把某行的 A 值从 11 更新到 55 之后，索引上它的位置会靠后；如果扫描器是按索引顺序往下扫，就有可能再“扫到”同一行一遍、又更新一次、又往后挪
- resolution1 ：只收集它们的旧值和新值，但不改表也不改索引；扫描结束后再修改

Chapter 14: Transactions

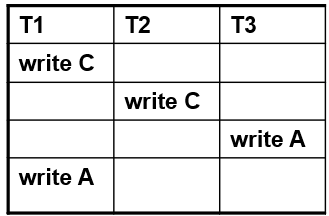
串行调度概念
- 串行调度（serial schedule） 要求：要么“先把 T₁ 的所有操作（包括提交）都做完”，然后再做 T₂；要么反过来先做 T₂ 再做 T₁。
- 非串行（not serial） 则说明两者的操作顺序被混合了——比如 T₁ 先写完 A ，接着 T₂ 读了 A ……然后 T₁ 再做 B 的读写，最后 T₂ 才做 B 的读写。
可串行化
- 冲突可串行化（Conflict Serializability）
  - 如果通过交换不互相冲突的操作顺序，就能把当前调度变换成一个串行调度，则称它是冲突可串行化。
  - “冲突”指对同一数据项、且至少有一个是写操作的两次访问。
- 视图可串行化（View Serializability）
  - 更宽松的标准：只要求每个事务读取到的值、以及最终数据项的写入顺序，与某个串行调度一致。
先行图
- 调度是冲突可串行化 当且仅当 其先行图无环。
- 无环时，通过拓扑排序可以直接得到一个等价的串行事务执行顺序。

视图可串行化

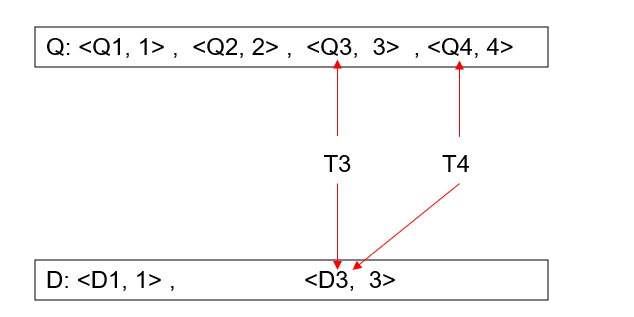
给定两个对同一批事务的调度 S 和 S′，称它们视图等价，当且仅当对任意数据项 Q，都满足下面三条：
- 初始读一致
- 读-写对应一致 : 如果在 S 中，某次 read(Q) 操作由事务 Tᵢ 执行，而它读到的是由事务 Tⱼ 的某次 write(Q) 所写的值，那么在 S′ 中，对应的那次 read(Q) 也必须读到事务 Tⱼ 的同一次 write(Q) 所写的值。
- 最终写一致
结果上来看，需要 1. 写回数据库的值是要和串行一样的（对应write） 2. 返回给应用的值是一样的（对应read）

可恢复调度

如果某事务 T_j 读取了另一个事务 T_i 写过的数据项 Q（即存在读—写冲突，并且 T_j 的 read(Q) 在 T_i 的 write(Q) 之后），那么 T_j 必须在 T_i提交（commit）之后才能提交。

级联回滚

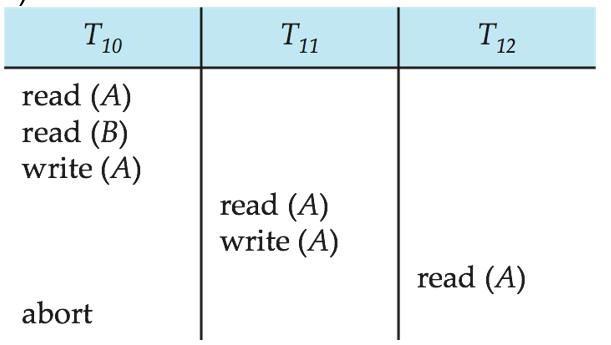
性能灾难：一次小小的事务失败，可能会让整个依赖链上的数十、数百个事务全部回滚，浪费大量计算和 I/O。(引出严格调度，无级联调度，两阶段封锁协议)
无级联调度禁止事务之间读脏数据，严格调度禁止一切读脏数据

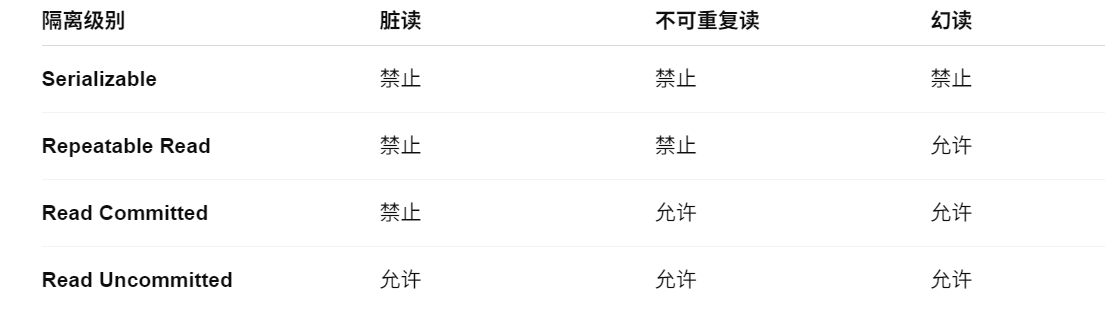
不可重复读：同一行两次读到的值不同
幻读：同一查询两次返回的行数或内容不同
Serializable（串行化）：这是最严格的隔离级别，它不仅能防止脏读、不可重复读，还能避免幻读

Chapter 15 : Concurrency Control

Lock-compatibility matrix

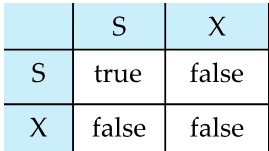
如果冲突（比方说请求 X‐锁，而有人持有 S‐锁或 X‐锁），就让该事务阻塞，直到冲突锁被释放。

两阶段封锁协议不一定能避免可恢复，要严格
两阶段封锁协议不一定能避免幻读，除非加范围锁

如果事务按照两阶段封锁协议进行的话，不可能有环状数据依赖（归谬）

（前提提示，事务已经按照两阶段封锁协议排布好了）

已知，有两个事务 Ti 和 Tj ，它们在某个数据项 D 上产生冲突，在先行图中存在一条从 T_i 指向 T_j 的有向边
接下来证明：冲突依赖 Ti→Tj 蕴含 LP(T_i)<LP(T_j)
- 假设冲突发生在数据项 D 上，那么有过程：
归谬，如果有环路，那么 LP(Ta)<LP(Tb)<LP(Tc)<⋯<LP(Ta) , 矛盾

方法2 归纳证明：前k-1个最小锁点的事务的先行图中没有环，再加上第k小锁点的事务，先行图中也不会有环

基本两阶段锁（Basic 2PL）此时只能保证冲突可串行化，但并没有强制“可恢复性”或“无级联回滚”。
冲突可串行化，但不遵守两阶段封锁协议

带有锁转换（Lock Conversions）的“两阶段锁（2PL）”变体

在传统严格的 2PL 中，一个事务一旦获得了某项数据的共享锁（S‐lock），如果它后来要写该数据，就必须等到放掉 S‐lock，再重新申请 X‐lock（排他锁）
- 为了减少不必要的释放与再次申请，现代数据库允许在 2PL 的阶段里 , 升级 ,降级

lock manager

锁不一定要跟着数据走（因为数据在外存/内存锁跟着走太麻烦了）
- 锁在一个地方统一管理最好(Lock Table)

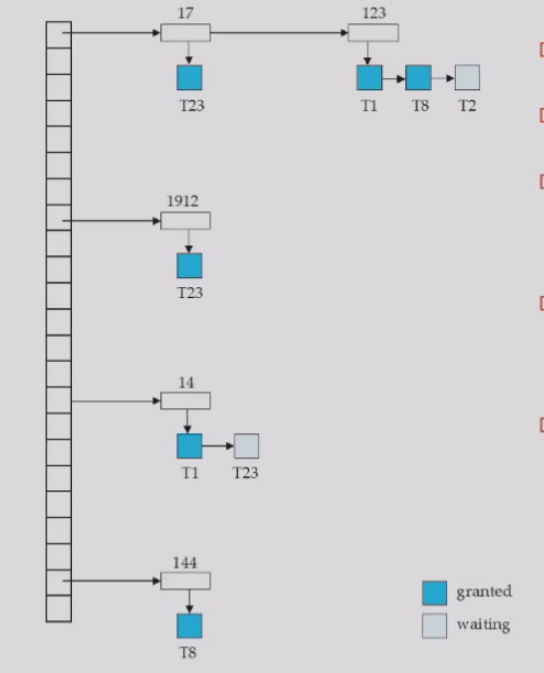
对于每一个 T_n ，也要建立一个表来看他拥有哪些数据的锁，方便释放时后根据这个表快速定位上述图片哈希表的内容

两阶段封锁协议无法避免死锁

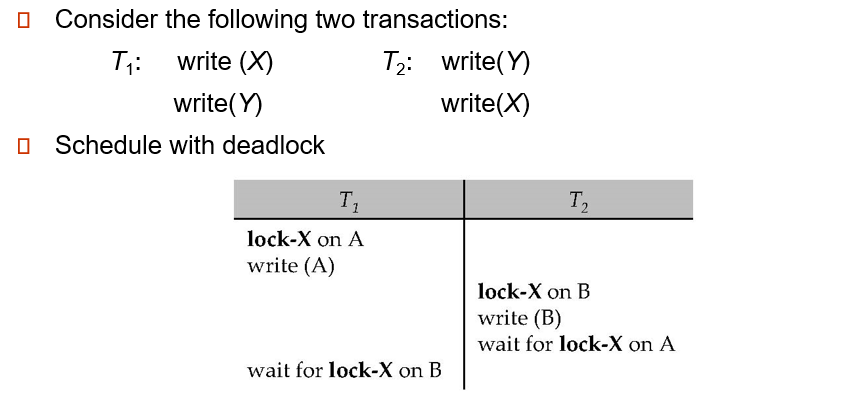
Deadlock Handling

死锁预防（Deadlock Prevention）
- 预先声明（Predeclared Locking）: 要求每个事务在真正执行之前，一次性申请它将要访问的所有数据项的锁
  - 并发度低，实际应用中很难知道所有可能访问的数据集
- 局部顺序（Partial Ordering）：在系统中为所有数据项 D1,D2,… 规定一个全局或局部的顺序， 任何事务只能按照这个既定顺序去申请锁
  - 并发度稍好一点
超时机制（Timeout-Based Schemes）
- 给等待锁的事务设置一个时限（timeout）
  - 可能出现饿死（Starvation）

Deadlock Detection

等待图（wait‐for graph）是随着事务进程实时更新的，一个事务指向另一个事务表示前一个在等后一个

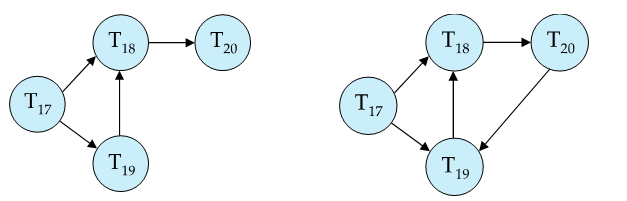
为了打破死锁，我们需要回滚其中一个事务，通常选择回滚最小代价的事务，即选择在循环中持有资源最少的事务。

Tree Protocol

只允许对数据项加排他锁（Exclusive Lock），不使用共享锁。
事务 Ti 第一次加锁时，可以选择对“树中任意节点”加锁，没有任何限制。
事务 Ti 在后续加锁时，只有当某个节点 Q 的“父节点”（在这棵事先定义好的树形结构中）已经被 Ti 保持锁定时，Ti才能对 Q 加锁。否则就必须等待。
事务可以在任意时刻释放（unlock）它所持有的锁；但是一旦 对某个节点 做过“加锁→解锁”操作，就 不允许再对该节点重复加锁。
整个树结构必须在系统启动时就全局固定好，也就是说：“谁是父节点、谁是子节点”这一层次关系，不允许在运行时改变。

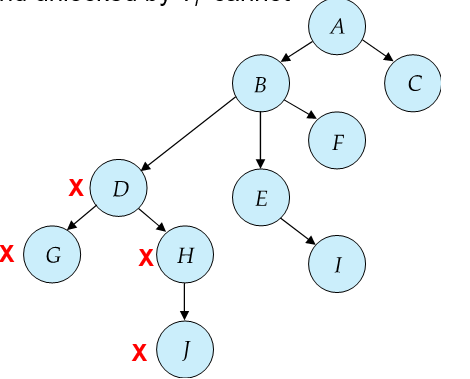
加 D ，加 G ，减 G ，加H , 减 D ，加J，减H , 减 J
- 保证冲突可串行化天然无死锁
- 不保证可恢复性（Recoverability）、无法自动避免级联回滚（Cascading Rollbacks）

Multiple Granularity(多粒度)

有了意向锁后，只需看“表”节点本身是否已有冲突的意向或实际锁，即可快速判定，无需深层扫描整个子树，效率大幅提升。
加锁是从根节点到叶子节点，解锁从叶子节点到根节点

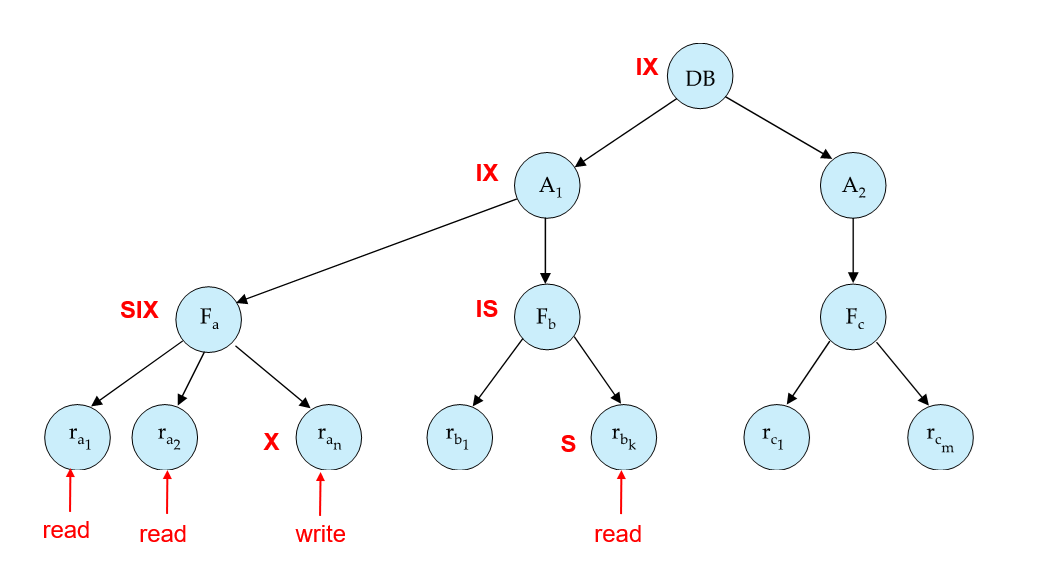
多版本并发控制（Multiversion Concurrency Control, MVCC）”

多版本并发控制的基本思路
- 每次写操作都不覆盖旧值，而是创建一个“新版本”。
- 每个历史版本都保留下来，供后续事务按照自己“读数据时刻”的需求去读取对应版本。
- 这样，读操作可以马上拿到与自己读时间相匹配的“老版本”数据，不必等待其他事务释放写锁；写操作只需在本事务提交时创建一个新的版本，也不必与读事务冲突。
- 只读事务永不阻塞 , 无需加锁，因为它不关心最新版本，只关心“时间戳 ≤ TS(Ti)”的历史快照
- 更新事务要对读操作加共享锁（S-lock），对写操作加排它锁（X-lock）

Lec 16 : Recovery System

写不动了，看学长的吧 Lec 15: Recovery System - NoughtQ的笔记本

若并发控制方案允许一个已被事务 T1 修改的数据项 X，在T1 提交前又被另一事务 T2 进一步修改，那么通过恢复 X 的旧值（即 T1 更新前的值）来撤销T1 的影响时，也会连带撤销 T2 的修改效果。为避免此类情况的发生，恢复算法通常要求：一旦某数据项被某事务修改，在该事务提交或中止前，其他事务均不得再修改该数据项。

当事务（即该事务的最后一条日志记录）的提交日志记录（即该事务的最后一条日志记录）被输出到稳定存储器时，我们称该事务已提交(committed)

basic

commit 不一定要把数据写到磁盘，可以写入buffer，使得系统更加灵活；但 log日志一定要写出去(不是commit也要提交)
checkpoint是为了记录log之上有哪些修改过的值还在buffer里，然后将他们写入磁盘，（但并非commit！后续如果有意外checkpoint之前的操作亦有可能被滚回！【为了保持只有commit才会提交的原子性】）记录他们的状态；使得 crush 的时候可以从这里以后开始 redo 和 undo
- 这样redo 就更短
  - 重做（redo）的目的
    - 1. 是为了得到完整的撤销列表；首先初始化撤销列表为checkpoint，然后向下重做；如果有<Ti start> 则加入相应事务，如果有<Ti commit> / <Ti abort>则移除撤销列表
    - 2. 对于那些有 <Ti commit> / <Ti abort> ，重做是为了确保它们在磁盘上缺失已经

Log-Record Buffering

之前的log不是commit也会提交，现在为了避免过多io，每一次commit数据前会提交log
在主存中的数据块输出到数据库之前，与该数据块中数据相关的所有日志记录必须已经输出到稳定存储器中——这一规则被称为写提前日志(write-ahead logging, WAL) 规则

Fuzzy Checkpointing

禁止写入的时间缩短，当modified block对应的log被完全写出之后，modified block这些data还未完全写出时就可以向另外块写入
维持一个 last_checkpoint

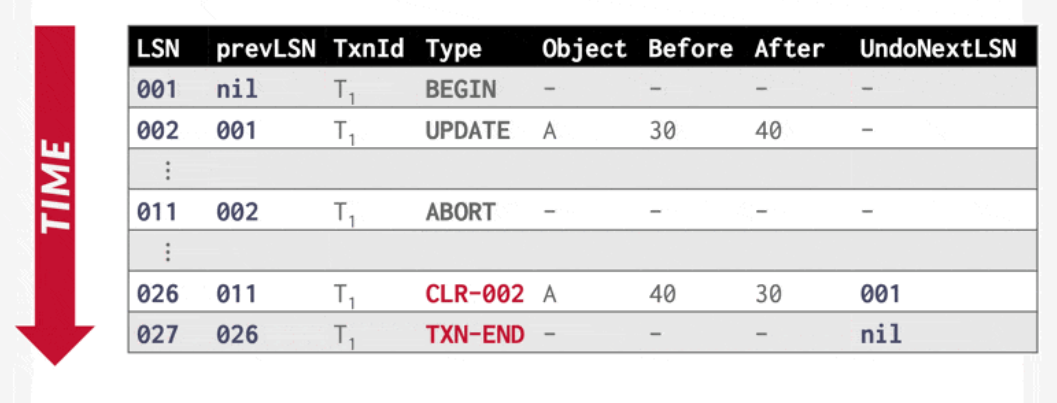
ARIES

前提提示：每条日志记录都有一个唯一的 LSN （log sequence number）；补偿日志记录(compensation log records, CLR)
- 基于CLR的，每个事务在某一时刻只能拥有一个 UndoNextLSN

checkpoint包含 ATT ,DPT ，DPT（dirty）记录每个page及其对应recLSN，即检查点之后的最早的脏页面修改，recLSN和checkpoint之间的部分能够避免redo

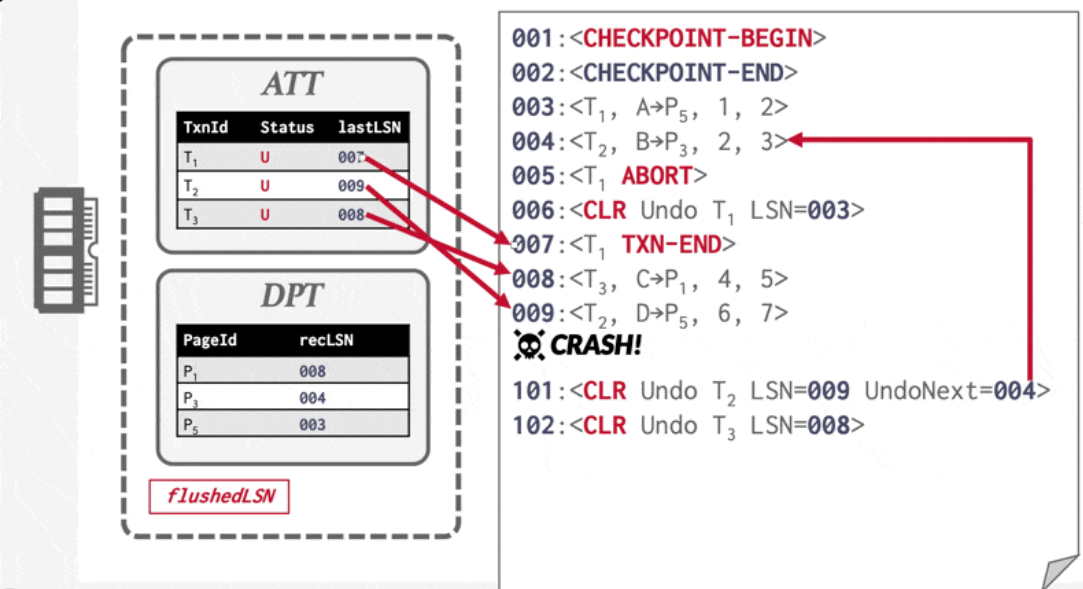
analysis pass

设置 redoList
在checkpoint 的基础上撤销列表
analysis过程中，也有可能再在脏页面中加入未记录的脏数据
- 为什么要加入？
  - 对于所有显式的commit，系统有可能只是把它放在了缓冲区，并没有实际提交到磁盘；而checkpoint会对以前commit的事务进行实际写到磁盘；而对检查点之后的部分，有些事务可能提交了但没有刷入磁盘，因此应该也加入dirty page，方便redo

redo pass

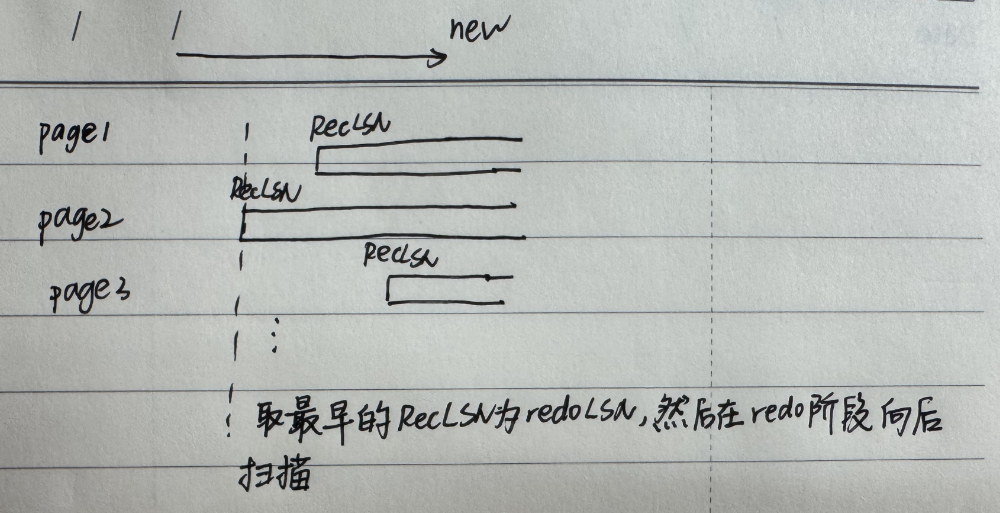
每当发现更新日志记录时，会执行以下操作：
- 若目标页不在 DirtyPageTable 中，或该更新日志记录的 LSN 小于 DirtyPageTable 中对应页面的 RecLSN 值（即图片中的那些短的page的空出来部分可能会被扫到），则跳过此日志记录；
- 否则重做阶段会从硬盘读取该页，若其 PageLSN 小于当前日志记录的 LSN，则重新执行该日志记录。【这里应该对应steal策略了】

undo pass（类似于非ARIES的undo）

根据撤销列表开始撤销
- undo期间，每个日志都会产生补偿日志记录，往往是上一条回滚日志对应的补偿日志记录对应的prevLSM
就看 ATT

三个操作的范围（undo应该也是整个的，这里没体现出来，redo整个，analysis在checkpoint之后向后）

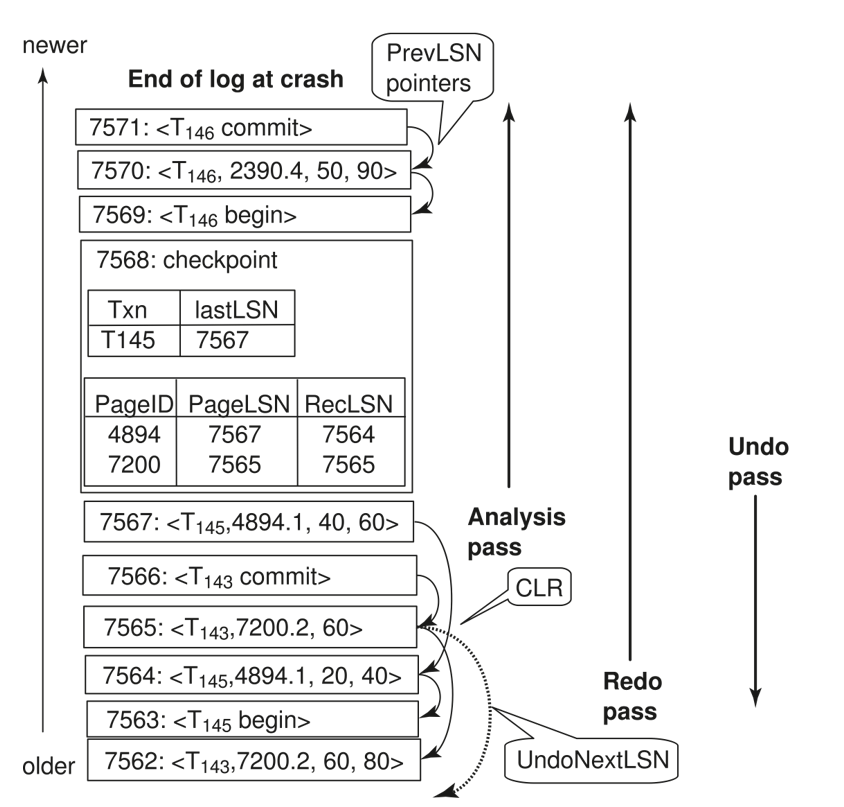
这张图中 143 事务在checkpoint之前已经提交了，而且经过checkpoint，143作的所有操作都永久化到磁盘了，而且page7200只经过事务143修改，说明page7200 的修改都永久化到磁盘了；为什么在checkpoint里的dirty page 仍然要加上pageID为7200 的脏页面来作redo？
- ARIES 采用的是 fuzzy checkpoint策略，7200可能还未写入磁盘后面的崩溃就开始了，因此需要redo

ARIES vs basic

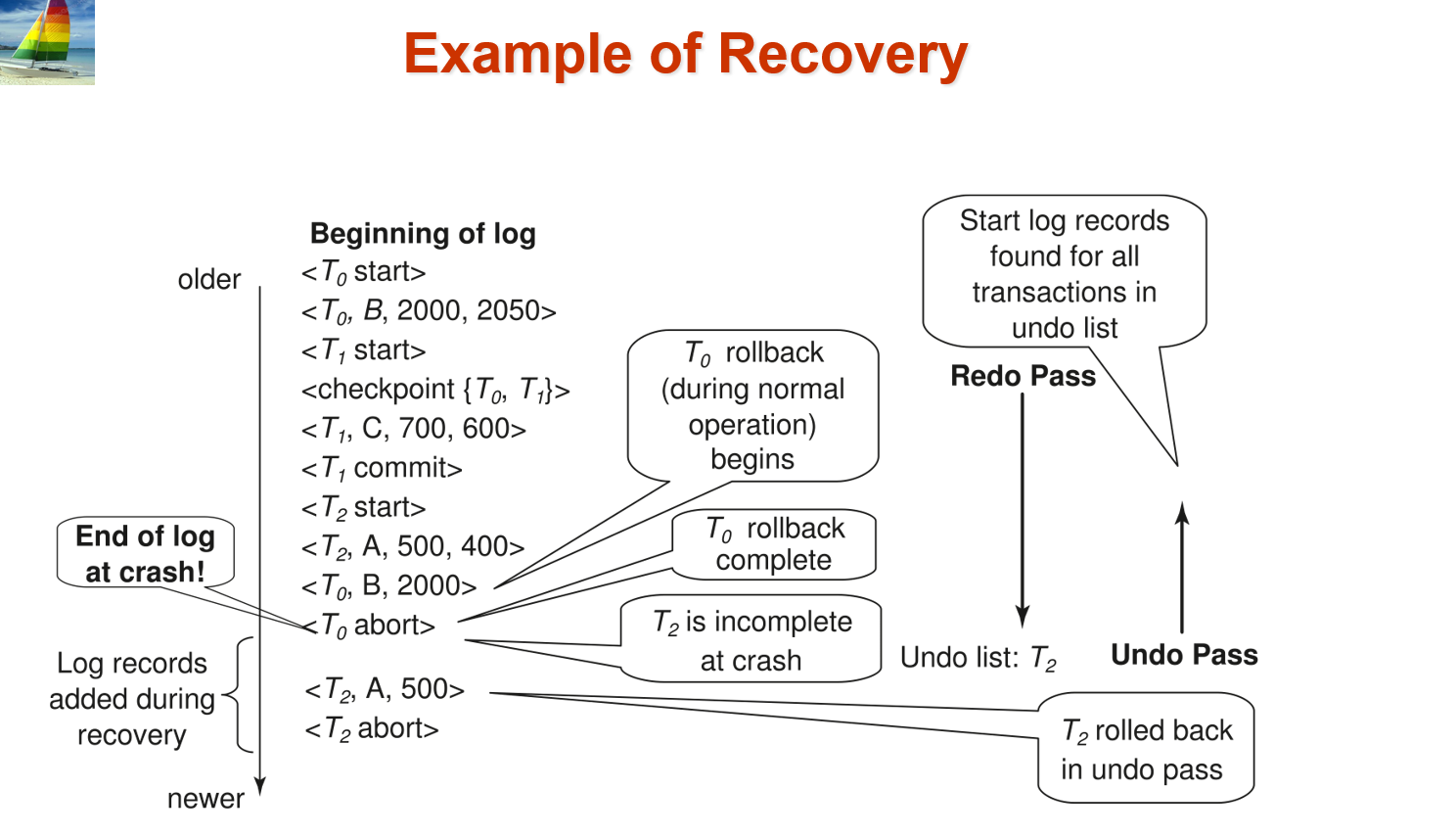
- basic 只有从 checkpoint 开始（假如不采取fuzzy）的 redo 和活跃事务的 undo；
  - Redo 事务：需要重做的事务是那些在崩溃前已经提交，但其操作尚未持久化到数据库中的事务。
    - 与ARIES不同，这里从checkpoint开始作redo，并且是按照事务来选择是否redo的
    - redo 范围是 checkpoint以后，undo则有可能到 checkpoint 以前
  - Undo 事务：需要撤销的事务是那些在崩溃前没有提交的事务。

Logical Undo

Lec 15: Recovery System - NoughtQ的笔记本

2017 历年卷

前者表示任意一条满足就行了，而不是所有的消费记录都在c0002的包含之内

左右两边natural join，假设join的对象两侧值都一毛一样，则是n*n；如果一侧分为k种类，则变成n*n/k; 如果两侧都分为k种类，还是n*n/k;
l_r: 每个元组的大小。 f_r: r 的 封装因子，即一个磁盘块能够容纳的 r 元组的数量。

2023 历年卷

判断题 1

×
在典型的 OLTP（Online Transaction Processing）场景中，往往是一条记录的多个字段要同时被修改（例如更新用户资料：姓名、地址、电话都要一起改）。这种操作被称为“行级更新”——一次事务会改动同一行里的多列。既然列存把每一列单独存放，更新一条记录时，如果要修改多列，就要分别访问每个列文件，进行随机写入（甚至可能打标记再合并），才能把那一行在所有列存储文件里的相应位置都更新。这会带来很多随机 I/O 和额外的开销，性能很差。

判断题2

×
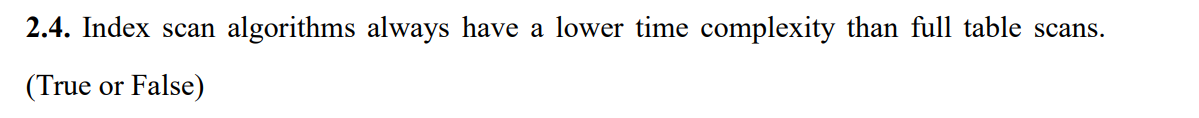
如果要查M个元素，当M接近 N 的时候 O(logN)+O(M)≈O(N). 不符合

判断题3

√
select只取部分的话，可以提前投影

不能AVG(COUNT(*))，要分开写

SELECT
  u.user_id,
  u.name,
  COUNT(f.follower_id) AS num_followers
FROM
  "user" AS u
  LEFT JOIN followship AS f
    ON u.user_id = f.user_id
WHERE
  u.group_name = 'game'
GROUP BY
  u.user_id,
  u.name
HAVING
  -- “当前用户粉丝数” 要大于 “game 组用户的平均粉丝数”
  COUNT(f.follower_id) > (
    -- 子查询：算出 game 组里所有用户的粉丝数平均值
    SELECT
      AVG(sub.num_followers)
    FROM (
      SELECT
        u2.user_id,
        COUNT(f2.follower_id) AS num_followers
      FROM
        "user" AS u2
        LEFT JOIN followship AS f2
          ON u2.user_id = f2.user_id
      WHERE
        u2.group_name = 'game'
      GROUP BY
        u2.user_id
    ) AS sub
  );

注意sub

2022历年卷

2020历年卷

T1

CHAR(10) 总是占用 10 个字符的空间，即使存储的字符串长度小于 10；而 VARCHAR(10) 只占用实际字符的空间，适合存储长度不定的字符串
- primary key (pID) 以及 foreign key (?) 一定要加括号
注意两个元素当作primary key的写法
- 注意check （？）

T6

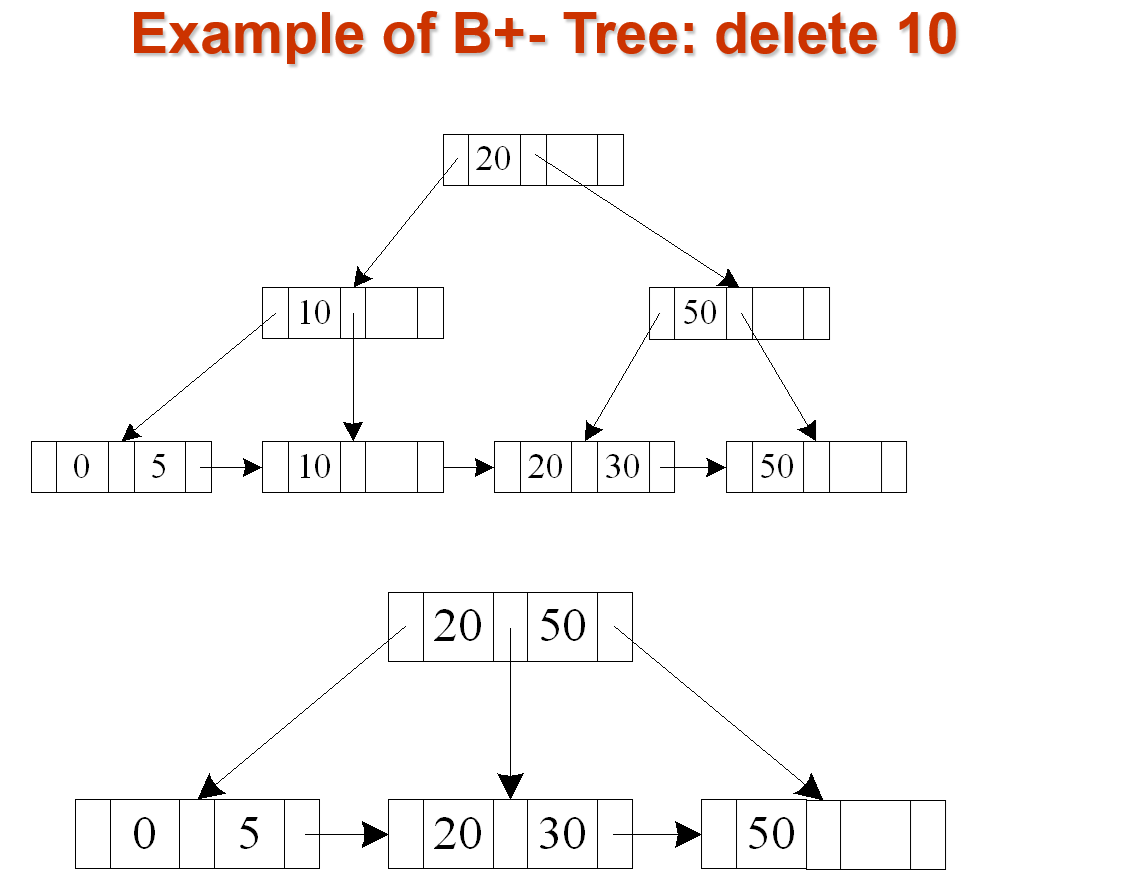
必须要邻居节点之和大于最大容量（等于也不行！），才能redistribute，不然只能merge

2019 历年卷

注意group by 之后只有被group by 的那个元素和聚合后的元素能被 select，其他就算每个group中的值一样的元素，也不能直接 select
- T1
T3 为了避免冗余、简化判断，业界和教科书都会先做极小覆盖，再做分解
T6
- （1）b 注意 client和project是多对多的，然后client 先求出其选择结果，就是大小为5，V=5 的；然后和project进行join 5*2000/max(5,400) = 25; 然后注意到 participate和employee的join，由于合并的项是employee外键，其合并结果等于participate 的个数 40000；再求以上两个join的join 25*40000/max(25,2000) = 500
- (3) 注意到，1. Bb的计算，要记得输出快也是Bb大小的 2. nh是除以Bb之后的结果
T7
- 1. 注意 WAL ，任何数据刷到磁盘之前，log必须刷到磁盘
- 2. 反正 checkpoint后面提交的都要重做

分享

数据库系统