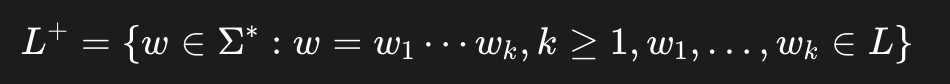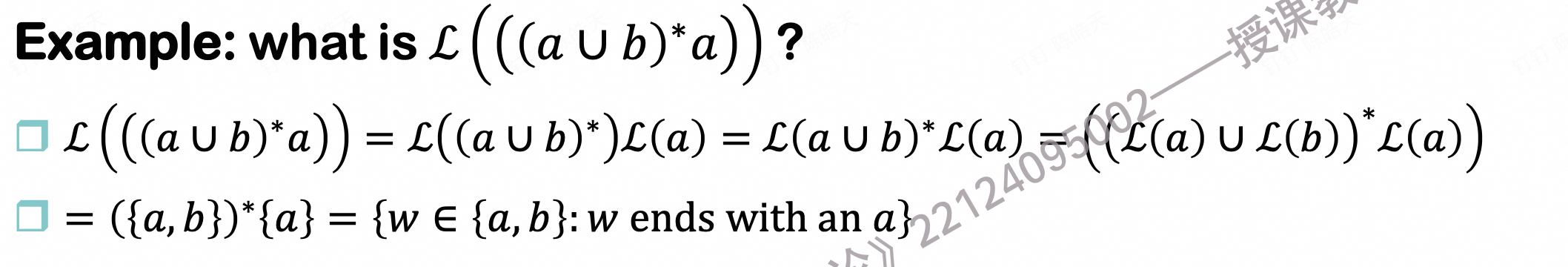Ch1．Sets, Relations, and Language

1.7 Alphabet and Language

1.7.1 Basic Concept

在计算理论中：

• 字母表 (Alphabet, Σ) 是一个非空的有限符号集合。例如，Σ = {0, 1} 就是一个二进制字母表。

• 字符串 (String/Word) 是由字母表中的符号组成的有限序列。例如，0110 是基于字母表 {0, 1} 的一个字符串。

• 语言 (Language, L) 是在某个字母表 Σ 上所有可能字符串的集合（这个所有可能字符串的集合被称为 Σ*）的一个子集。

1.7.2 Operations of Languages

• 基本集合运算

  • 并 (Union)、交 (Intersection)、差 (Difference)、补 (Complement)

    • 这些运算和标准的集合运算完全一样。

    • 补集 (Complement) 的定义是 L̄ = Σ* - L。这里的 Σ* 指的是由字母表 Σ 中所有符号能够构成所有可能字符串的集合（包括空字符串）。L 的补集 L̄ 就是 Σ* 中所有不属于 L 的字符串的集合。

• 幂运算 (Exponentiation)

  • 这是一个递归定义：

    • L⁰ = {e}：语言 L 的 0 次幂，是一个只包含空字符串 e（有时也写作 ε 或 λ）的语言。

    • Lⁱ⁺¹ = LLⁱ：语言 L 的 i+1 次幂，等于 L 的 1 次幂与 L 的 i 次幂的连接（Concatenation）。

    • 简单来说：

      • L¹ = L

      • L² = LL (L 中任意两个字符串前后拼接)

      • L³ = LLL (L 中任意三个字符串前后拼接)

• 连接运算 (Concatenation)

  • 

• Kleene Star L*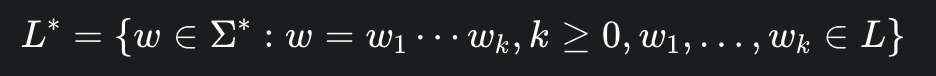

  • 

  • 

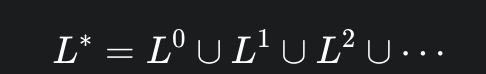
  • 关键点：k ≥ 0 任何语言的克林闭包 L* 一定包含空字符串 e。

• Kleene Plus L⁺

  • 

  • 

1. Q: (空字符串 e 是否可能属于 L⁺？) 可以，让e属于L, 通过一次拼接可得

2. Q: (在什么情况下 L⁺ 会等于 L*？) 当且仅当原始语言 L 包含空字符串 e 时

1.8 Finite Representations of Language

What is Finite Representations?

• 本身必须是一个字符串 ; 不同语言应有不同表示

1.8.1 Definition: The regular expressions

① 基础情况 ： ∅ {x} (对于 ∀x ∈ Σ) 是一个正则表达式(Σ是字母表)

② 归纳步骤 : 假设 α 和 β 都已经是合法的正则表达式 , 那么下面三种方式构建的新字符串也都是合法的正则表达式: (αβ) (α ∪ β). α*

• 

• 语言L无法被正则表达式描述，揭示了正则表达式表达能力有其边界；

1.8.6 Regular expressions & languages

如何通过正则表达式推出其想表示的语言？

1. 基础情况 ℒ(∅) = ∅ , ℒ(a) = {a} (左边的 a 是一个只包含单个符号的正则表达式。)

2. 递归步骤 ℒ(αβ) = ℒ(α) ℒ(β). ℒ(α|β) = ℒ(α) ∪ ℒ(β). ℒ(α*) = (ℒ(α))*

   1. 如果 α = a，β = b，那么 ℒ(ab) = ℒ(a)ℒ(β) = {"a"}{"b"} = {"ab"}

   2. 如果 α = a，β = b，那么 ℒ(a|b) = ℒ(a) ∪ ℒ(β) = {"a"} ∪ {"b"} = {"a", "b"}。

   3. 如果 α = a，那么 ℒ(a) = {"a"}。ℒ(a*) = ({"a"})*

1.8.7 Remark

1. 任何一个可以用正则表达式表示的语言，也都可以用无穷多个其他的正则表达式来表示(多对一关系)。

语言 L = {"a"}: 正则 : a , a|a , a|a|a , etc.

区分 | 和 ∪

1. 正则表达式 R1 = gray 所描述的语言是 L(R1) = {"gray"}。

2. 正则表达式 R2 = grey 所描述的语言是 L(R2) = {"grey"}。

3. 我们将这两个正则表达式用 | 组合起来，得到新的正则表达式 R3 = gray|grey。

4. 那么，新正则 R3 所描述的语言 L(R3) 是什么呢？它就是两个子语言的并集： L(R3) = L(R1) ∪ L(R2) = {"gray"} ∪ {"grey"} = {"gray", "grey"}

Ch2．Regular Language and Automata

2.1 Deterministic Finite Automat

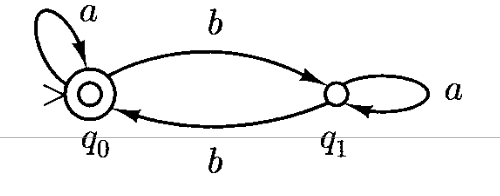
2.1.1 Definition

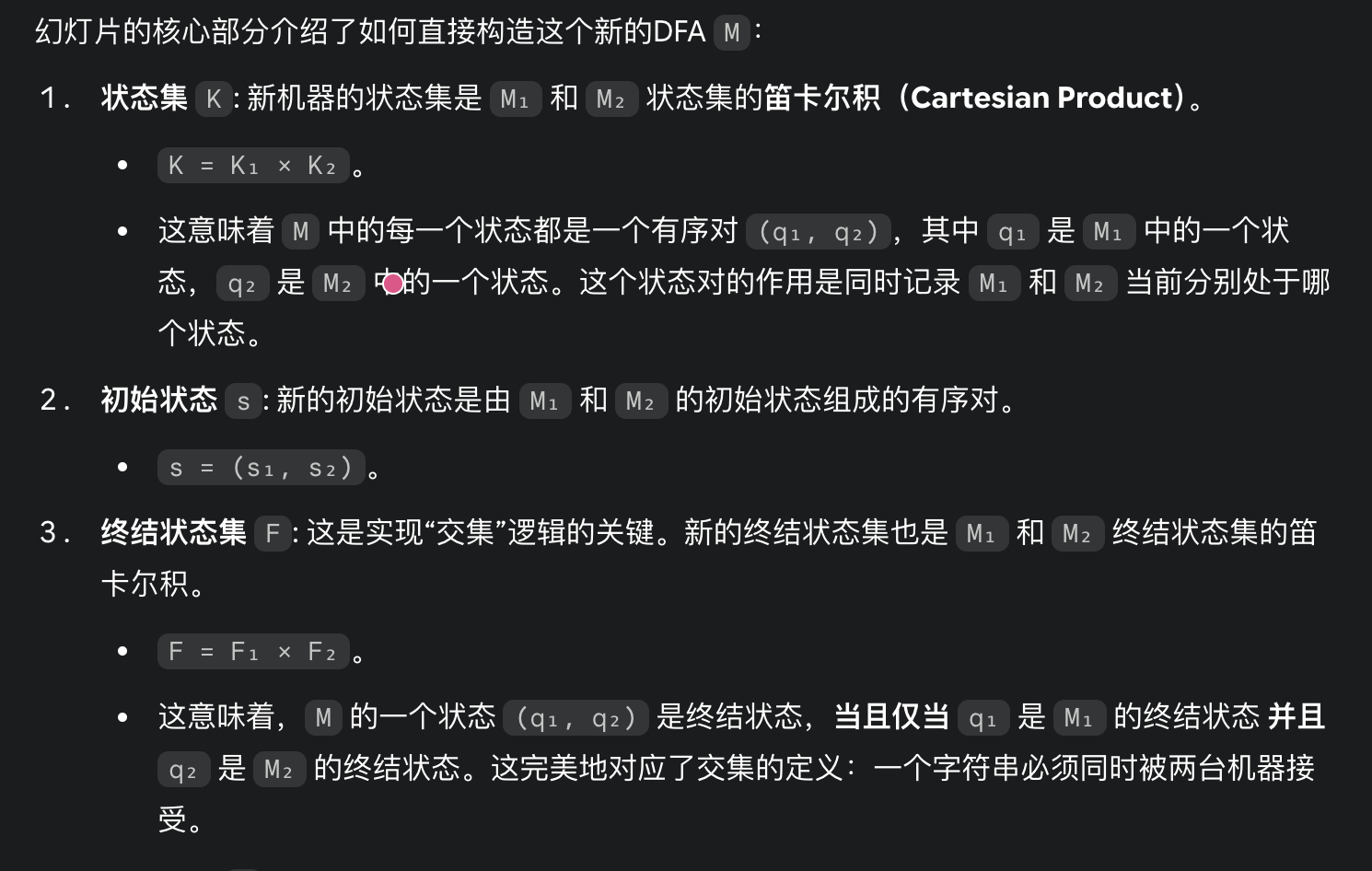
• A deterministic finite automata (DFA) is a quintuple (K, Σ, δ, s, F), where

  • K 状态集合 这个DFA所有可能状态的集合。这个集合必须是有限的。

  • Σ - 字母表 (An alphabet)

    • 这个DFA能够识别的所有输入符号的集合。

  • δ - 转换函数 (Transition function)

  • s (或q₁) - 初始状态 (The initial state)

  • F - 终止状态集合 (The set of final states)

• 一个语言的DFA和它的补集语言的DFA之间存在简单的转换关系。

  • 只需要把这个DFA中所有的终止状态变成非终止状态，所有的非终止状态变成终止状态，就能得到一个识别 L₂ (包含"bbb") 的DFA。

2.1.2 Configuration And Yield

1. 格局为DFA在计算过程中的一个快照, 保存以下信息： 当前状态、未来要读的输入

2. 如果 (q, w) 能在一步之内产生 (q', w') ，那么 (q, w) ⊢ (q', w')

3. ⊢_𝑀^∗ is the reflexive, transitive closure of ⊢_𝑀

   1. 自反性 (Reflexive)：任何格局都可以“经过零步”到达它自身。

   2. 传递性 (Transitive)：如果格局A能一步到达格局B，格局B能一步到达格局C，那么我们就可以说格局A能“经过多步”到达格局C。

4. A string w ∈ Σ* is said to be accepted by M iff there is a state q ∈ F such that (s, w) ⊢* (q, ε).

5. 自动机的语言L(M): L(M) is the language accepted by M and is the set of all strings accepted by M.

2.2 Nondeterministic Finite Automata

• 目标语言 L: (ab ∪ aba)*

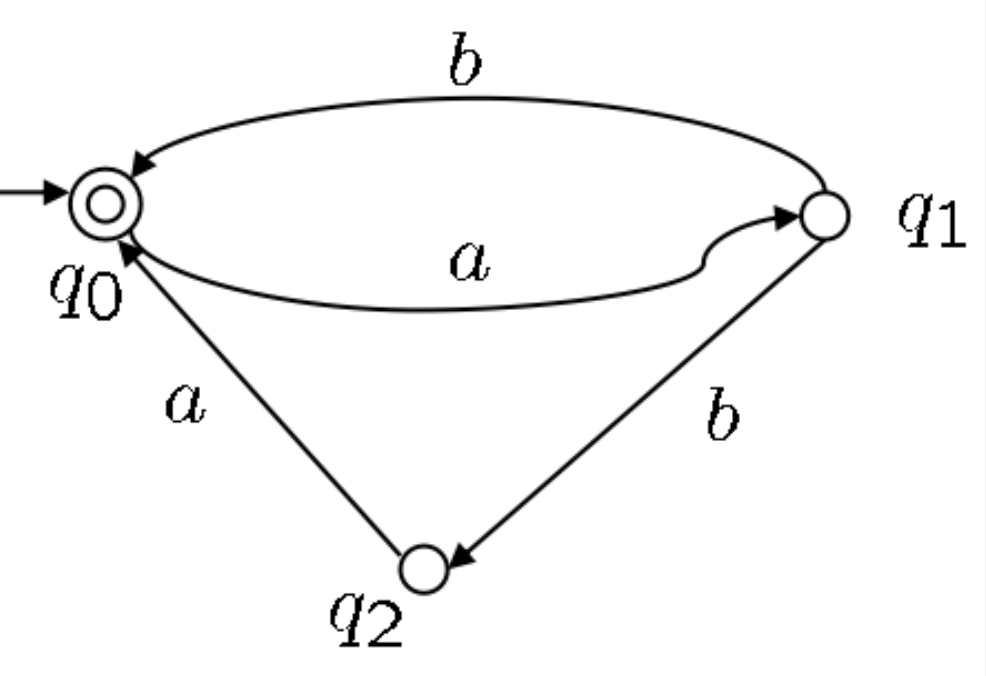
• 这种在某个（状态，输入符号）组合下，存在多个可选的下一状态的情况，就是“非确定性”

• NFA的接受规则是：只要存在至少一条路径能够走通，并最终停在终止状态，那么这个字符串就被接受。

2.2.1 Definition

1. (K, Σ, Δ, s, F) , K 为状态集合 ，Σ为字母表， s为初始状态， F为终止状态的集合 ， 关键区别在于Δ，为转换关系

2. 对比： DFA 的 δ 是一个函数：δ: K × Σ → K

3. Δ 是 K × (Σ ∪ {ε}) × K 的一个子集，这意味着可以同时包含 (q, a, p₁) 和 (q, a, p₂) 这样的元组, 并且允许ε 转换

• 由 a, b 构成的字符串，其中包含子串 "bb" 或者 "bab"

  • 

• 在一个至少包含2个符号的字母表 Σ 中，该语言包含了所有至少缺少一种字母表中符号的字符串。

  • 

• 倒数第6个符号是 a

  • 

2.2.2 Expressive power: NFA vs. DFA

1. 每个DFA都是一个NFA

2. NFA允许更多的转换

3. 对于任何一个由NFA M 所能识别的语言 L，必然存在一个对应的DFA M'，它也能识别完全相同的语言 L。

2.2.3 Make equivalence

• definition of DFA/NFA equivalence

  当且仅当两个有限自动机 M₁ 和 M₂ 所接受的语言完全相同时 (L(M₁) = L(M₂))，我们才说它们是等价的。

• 转化NFA 为DFA算法

1. 给定 (Given)：一个 NFA M = (K, Σ, Δ, s, F)目标构造 (Construct)：一个等价的 DFA M' = (K', Σ, δ', s', F')

2. DFA M' 各部分的定义

   1. 新的状态集 K' = 2^K : 新的DFA中的每一个状态，都对应原始NFA中的一个状态的集合。这正是我们用来解决“多重选择”问题的关键。如果一个NFA在某个时刻可能处于 {q₀, q₁} 两个状态，那么新的DFA就在一个名为 "{q₀, q₁}" 的单一状态里。

   2. 新的初始状态 s' = E(s) (E(s) 是 s 的 ε-闭包 (epsilon-closure) ): 新的DFA的起始点，不仅包含NFA的起始状态 s，还包括所有从 s 出发仅通过 ε-转换（免费跳转）就能到达的所有状态。

   3. 新的终止状态集 F' : 只要DFA的某个“集合状态”中，包含了至少一个NFA原来的终止状态，那么这个“集合状态”就是DFA的一个终止状态。

   4. 新的转换函数 δ' : 如何计算从DFA状态 Q 经过输入 a 到达的下一个状态?

      1. 步骤 A: 真实移动 (Move) 首先，找出从 Q 集合中的每一个状态 q 出发，在读取了输入符号 a 之后，根据NFA的规则 Δ 能到达的所有状态 p。将所有这些 p 汇集到一个临时的集合中。

      2. 步骤 B: ε-闭包 (Closure) 然后，计算上一步得到的那个临时集合的ε-闭包。也就是说，从那个集合里的所有状态出发，再进行所有可能的“免费跳转”。最终得到的这个集合，就是DFA的下一个状态。

2.2.4 The Key Claim

1. 等式左边：NFA 的计算; NFA M 从状态 q 开始，在读完整个字符串 w 后，存在某条路径可以最终到达状态 p。

2. 等式右边: 通过子集构造法生成的那个等价 DFA M' 的行为;

   1. DFA M' 从它的初始状态 E(q) 开始（这个状态是 NFA 初始状态 q 的 ε-闭包）。

   2. 在读完整个字符串 w 后，DFA M' 最终到达了它的某个状态 P。（记住，DFA的状态 P 本身是一个NFA状态的集合）。

   3. 并且，NFA的那个终点状态 p，正好是DFA最终到达的这个集合 P 中的一个成员 (p ∈ P)。

2.3 FA & Regular Expression

2.3.1 Key Theorem

一个语言 L 是正则的，当且仅当存在一个有限自动机 M 能够接受它。换句话说，有限自动机能识别的语言集合和正则语言所描述的语言集合是完全相同的

2.3.2 Proof

证明思路：

方向一：从正则表达式到有限自动机；为最基本的正则表达式（如单个字符、空集）构建基础的FA。为复合的正则表达式（如并集 ∪、连接 ·、克林闭包 *），将已构造好的小FA组合成一个更大的FA。

方向二：将原始FA进行一些标准化处理（例如，确保单一的起始和结束状态）。通过归纳法，逐步消除自动机的中间状态，并将经过这些状态的路径用正则表达式来标记在状态之间的转换弧上。最终，当自动机只剩下起始和结束状态时，它们之间转换弧上的标签就是一个描述了整个自动机所接受语言的正则表达式。

2.3.2.1 对于正则表达式的每一种构造规则，我们都有一个对应的方法来构造或组合FA。

我们可以通过一个递归的过程，根据正则表达式自身的定义来一步步地构建出对应的FA。

这个定义告诉我们，所有复杂的正则表达式都是由最简单的部分通过这三种运算组合而成的。因此，证明思路就是去证明FA在三种核心运算下是封闭的

1. 并集 (Union)

目标：给定两个NFA，分别为 M₁ 和 M₂。我们需要构造一个新的NFA M，使得 M 接受的语言 L(M) 是 M₁ 接受的语言 L(M₁) 和 M₂ 接受的语言 L(M₂) 的并集。

• L(M) = L(M₁) ∪ L(M₂)

"Is infinite unions regular?" (无限个正则语言的并集还是正则的吗？)

• 答案：不一定。

• 解释：上述构造方法只适用于有限次并集。虽然任何有限个正则语言的并集仍然是正则的，但无限个正则语言的并集可能不是正则语言。

• 一个简单的例子：考虑一系列正则语言 L₁ = {a¹b¹}, L₂ = {a²b²}, L₃ = {a³b³}, ... 每一个 Lᵢ 本身都是只包含一个字符串的有限语言，因此是正则的。但是，它们的无限并集 L = ∪ Lᵢ = {aⁿbⁿ | n ≥ 1} 是一个经典的非正则语言。

2. 串接 (Concatenation)

目标：给定两个NFA，分别为 M₁ 和 M₂。我们需要构造一个新的NFA M，使得 M 接受的语言 L(M) 是 M₁ 接受的语言 L(M₁) 后面紧跟着 M₂ 接受的语言 L(M₂)。

• L(M) = L(M₁) L(M₂)

3. 克林闭包（Kleene Star）

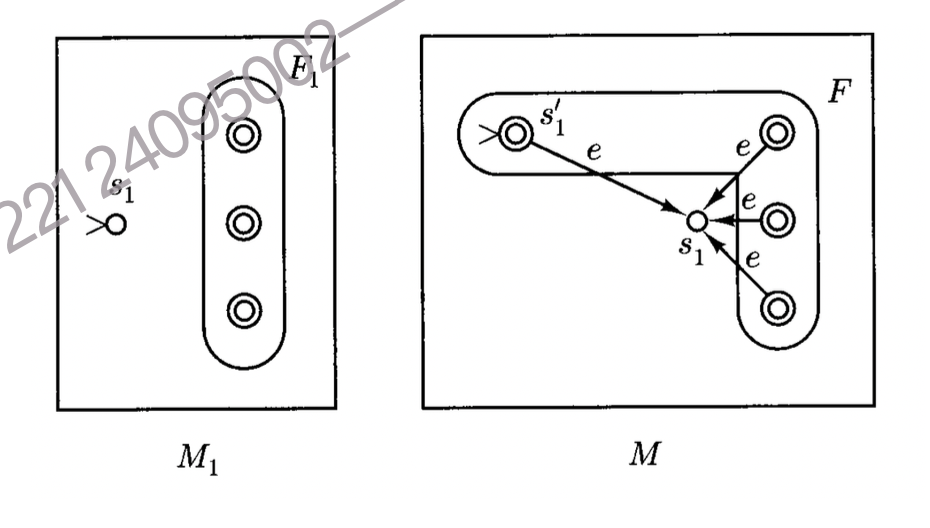
1. Why do we need to make the new initial state also a final state?

为了接受空字符串 e。

2. Why can't skip the introduction of the new initial state?

因为如果仅把原来的起始点设为终点，会产生意料之外的后果

eg. 已知 𝐿(𝑀) = 𝑎 (𝑏𝑎)^∗

𝐿(𝑀)* = (𝑎 (𝑏𝑎)^∗)^* 这样表示是错的

额外接受了 ab

4. (额外的) 补集 (Complementation)

只需要改变 终结状态集 F: 这是唯一也是最关键的改变。新机器 M 的终结状态集是原机器 M₁ 中所有非终结状态的集合。F = K - F₁

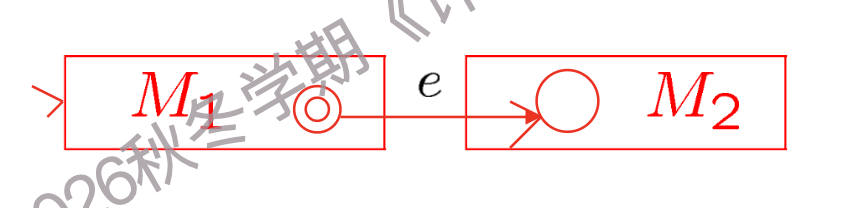
5. （额外的）交集（Intersection）

一个字符串只有在同时被 M₁ 和 M₂ 接受时，才会被新的机器 M 接受。

证明正则语言在交集运算下是封闭的 L(M₁) ∩ L(M₂) = Σ* - ((Σ* - L(M₁)) ∪ (Σ* - L(M₂)))。因为我们已经知道正则语言对补集和并集运算是封闭的，所以它们的交集也一定是正则的。

2.3.2.2 有限自动机（FA）转换为正则表达式（Regular Expression）

1. 将有限自动机（FA）转换为正则表达式所使用的一个关键中间工具——广义有限自动机（Generalized Finite Automaton, GFA 或 GM）。一个广义有限自动机 MG 是对普通NFA M 的一种推广。

• GFA的四大特征

  • 一个GFA有且仅有一个终结状态

  • 转换标签可以是正则表达式

  • 没有任何转换可以指向初始状态 ， 没有任何转换可以从终结状态出发

2. 广义有限自动机构造

• 这个过程旨在将任意给定的FA M 扩展成一个满足GFA所有特性的新机器 MG，同时不改变它所接受的语言。

2.3.2.3 将有限自动机（FA）转换为正则表达式 (证明方法2)

1. 定义

状态排序: 给定一个有 n 个状态的FA M，我们首先将它的所有状态排成一个序列，并用数字 1 到 n 进行编号，即 K: q₁, q₂, ..., qn。

核心定义 R(i, j, k): 幻灯片定义了 R(i, j, k)，它是一个字符串的集合。R(i, j, k) 代表的是所有能让自动机从状态 qi 走到状态 qj 的字符串的集合。

• 但这里有一个非常重要的限制：在这条路径上，所有经过的中间状态的编号都不能大于 k。

关键点：k 就像一个“许可”，它规定了路径可以使用哪些中间状态。k=0 意味着不能经过任何中间状态（只能是直接转换）；k=1 意味着可以经过 q₁ 作为中间状态，以此类推。起点 qi 和终点 qj 不算作“中间状态”，所以它们的编号可以大于 k。

2. 归纳法证明 (Proof: induction by k)

基础步骤 (Base case k = 0)

• 含义: k=0 意味着我们寻找从 qi 到 qj 的路径，且路径中不允许经过任何中间状态（因为所有状态编号都大于0）。

• 公式解释：

  • 如果 i ≠ j，R(i, j, 0) 就是所有能让机器从 qi 一步直接转换到 qj 的输入符号 a 的集合。

  • 如果 i = j，R(i, i, 0) 除了包含所有从 qi 直接转换回自身的符号 a，还必须包含空串 e，因为它代表了从 qi 到 qi 的零步路径。

• 结论: 无论哪种情况，R(i, j, 0) 都是一个有限的符号集合（可能加上 e）。任何有限语言都可以用正则表达式（例如 a ∪ b ∪ c）表示，因此基础情况成立：所有 R(i, j, 0) 都是正则的。

有人说，如果qi 到 qi 自己有一个 字符为a 到转移，那qi 到 qj 不是可以 有无限个a 的字符串了？实则不然，qi 到 qi 中，后一个qi 算中间状态了，而所有state 到 编号都大于 0，所以无允许中间状态，也不允许 QI 到 qi 了

归纳步骤 (Induction step)

• 归纳假设: 假设对于所有 i 和 j，R(i, j, k-1) 所代表的语言都是正则的。

• 目标: 证明 R(i, j, k) 也是正则的。

核心公式: R(i, j, k) = R(i, j, k-1) ∪ R(i, k, k-1) R(k, k, k-1)* R(k, j, k-1)

2.4 To show a language be Regular or Not Regular

2.4.1 Proof a language be Regular or Not Regular

eg.

• 目标： 证明一个语言 L 是正则的。

• 语言 L 的定义：

  • 

    1. 是非负整数的十进制表示。

    2. 没有多余的前导零（例如 "0" 和 "123" 可以，但 "05" 不行）。

    3. 这个数可以同时被 2 和 3 整除。

证明方法：

1. 证明它可以被有限自动机 (FA) 接受。

2. 证明它可以用正则表达式描述。

3. 利用正则语言的闭包特性 (Closure Properties)。

证明:

1. 定义 L1：所有合法的非负整数表示（没有多余前导零）

   • L1 = 0 ∪ {1, 2, ..., 9} {0, 1, ..., 9}*

   • 这个 L1 可以用正则表达式表示（如上所示），因此 L1 是正则语言。

2. 定义 L2：能被 2 整除的合法非负整数

   • 一个数能被 2 整除，当且仅当它的最后一位是偶数（0, 2, 4, 6, 8）。

   • 我们可以定义 L2 为 L1 与“所有以偶数结尾的字符串”的交集。

   • L2 = L1 ∩ ∑* {0, 2, 4, 6, 8}

   • 根据闭包特性 两个正则语言的交集也是正则的

3. 定义 L3：能被 3 整除的（十进制）数字字符串

   • 关键证明： 幻灯片展示了一个可以接受 L3 的有限自动机 (FA)。

   • 

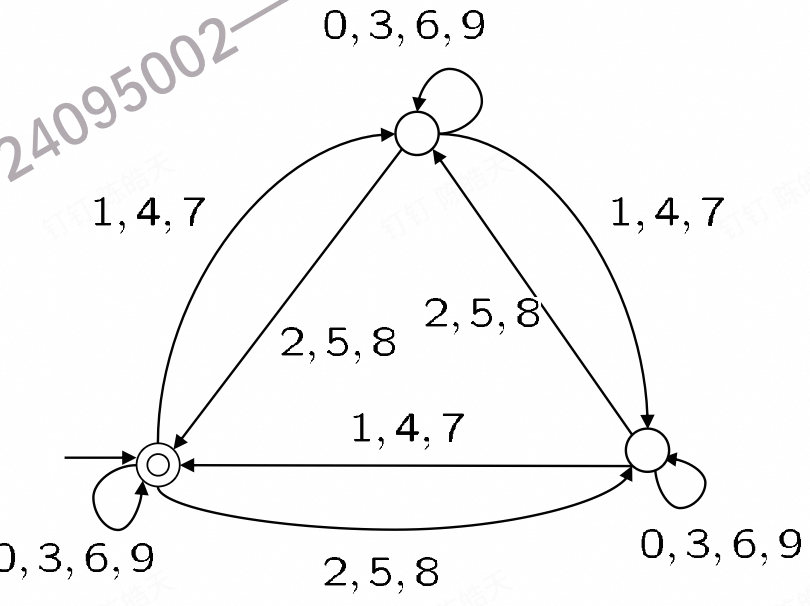
   • 因为 L3 可以被这个 FA 接受，所以 L3 是正则语言。

4. 因此， L = L2 ∪ L3 ,根据正则语言的闭包特性，两个正则语言的交集仍然是正则语言。

eg. 证明不是正则的证明 L = { ω ∈ {a,b}* : ω 中 a的数量等于 b 的数量} 不是正则语言

• 这里巧妙的运用了两个表达式的特性 , 构造了 aⁿbⁿ

2.4.2 为什么存在非正则语言

1. 直观解释

   1. 一个有限自动机 (FA) 只有有限个状态 (finite state)，所以它只能“记住”或“重复”有限多种事物。

   2. 例如 L = {aⁿbⁿ}, n 可以无限， 一个FA无法记住这么多状态

2. 数学解释

   1. 给定一个字母表 ∑（例如 {a, b}），所有可能的字符串集合 ∑* 是可数无限 (countably infinite) 的（就像自然数 1, 2, 3... 一样多）。

   2. ∑ 的所有子集的集合,是不可数无限的

   3. 因此,语言的总数是不可数的

   4. 一个正则表达式本身只是一个有限长度的字符串（由∑ 中的符号加上 ∪, *, (, ) 等构成）。

   5. 所有可能的正则表达式的集合是可数无限的

   6. 我们有不可数多个总语言, 但只有可数多个是正则语言; 因此，必然存在“（不可数 - 可数）= 不可数”个非正则语言。

2.4.3 泵引理

一个有限自动机 (FA) 的“内存”就是它所处的状态。因为状态是有限的（比如有 n 个状态）。如果 FA 接受一个“足够长”的字符串 w（比如 w 的长度 m > n），当机器处理这个字符串时，它会经过 n+1 个状态; 根据 鸽巢原理，必然至少有一个状态被重复访问；这种状态的重复（如图中 q_j = q_k）在 FA 的路径上形成了一个循环

泵引理的唯一用途是证明一个语言不是正则的，而不能证明一个语言是正则的

eg. 证明 L = {aⁿ, n是素数} 不是正则语言

1. 假设 L 是正则的。

2. AI 给出某个泵长度 n (n 已经蕴含"任意"这个条件了)

3. 我们选择一个字符串 w = a^m，其中 m 是一个素数且 m ≥ n。（这总是可能的，因为素数有无限个）。

4. AI 必须拆分 w=xyz ; 因为 w 只包含 a，所以 x, y, z 也都只包含 a。给出 x = a^p , y = a^q , z = a^r. 并且 p + q + r = m; 并且， q ≥ 1

5. 我们必须选择一个 i，使得“泵”后的新字符串 xyⁱz 不在 L 中 ; 选择 i = m+1 ,

eg. 证明 L = {uu^Rv | u, v ∈ {a, b}⁺} 不是正则的

1. 利用闭包特性简化

我们选择一个正则语言 L1 = (ab)⁺(ba)⁺. 然后定义 L' = L ∩ L1 , 如果 L 是正则的，那么L' 也将会是正则的；L' 的形式应该为 (ab)ⁿ(ba)ⁿ(ba)^m-n. (m > n >= 1)

2. 用泵引理证明 L' 不是正则的

AI 假设 L' 是正则的，给出泵长度 p ; 我方选择一个字符串 w ∈ L' , 如 (ab)^p(ab)^p+1 (由于 4p+2>p ,所以符合条件)

然后AI 将 w 拆分成 xyz的形式，𝒚 = (𝒂𝒃) ^𝒌 𝐨𝐫 𝒃 (𝒂𝒃) ^𝒌−𝟏𝒂 𝐨𝐫 𝒃 (𝒂𝒃) ^𝒌−𝟏 𝐨𝐫 (𝒂𝒃) ^𝒌−𝟏𝒂 分别验证 不符合条件

eg. 以下语言是否是正则的？

1. 可数个正则语言的并集 : 不一定

正则语言的闭包特性只保证有限 (finite) 个正则语言的并集是正则的。它不适用于可数无限 (countably infinite) 个。

考虑语言 L = {aⁿbⁿ}

2. 可数个正则语言的交集 : 不一定

考虑语言 L' = {aibi | i ≠ j } , 这是非正则语言; 但我们可以把它构造到一个可数的 正则语言的交集

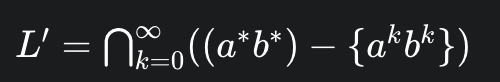3. 正则语言的子集不一定是 正则语言

Ch3．Context-free Language and Pushdown Automa

3.1 Context-Free Grammars

3.1.1 定义

1. CFG 是一个 4 元组 G = (V, ∑, R, S), 它是一个生成设备

   1. V 变量 (Variables) 字母表 （终结符和非终结符的并集）

   2. ∑ 终结符 (Terminal symbols) 字母表（即语言中真正出现的字符，如 'a', 'b'）

   3. R 一组有限的规则 (Rules)

   4. S 起始符号 (Start symbol)（一个特殊的变量) [ 必须是一个非终结符 ]

2. Notation: (例如 S -> aSb 在数学上等同于 (S, aSb)存在于 R 中 )

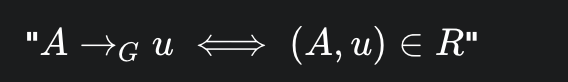
3. 单步推导 (one-step derivation)

4. 多步推导 (multi-step derivation)

• 语言 L 是 CFL，当且仅当它被一个 CFG 生成。

• 语言 L 是 CFL，当且仅当它被一个 PDA (下推自动机) 接受。

3.1.2 证明一个文法 G 所生成的语言 L(G)，与一个给定的语言 L 是相等的

1. 目标，证明 某个 L(G) = L, 其中, L = {w ∈ {a, b}* , a b 数量相等} ; CFG G, 有 S ⇒ SS, S ⇒ aSb, S ⇒ bSa, S ⇒ e

2. 先证 w ∈ L(G) ⇒ w ∈ L

   1. 基础情况，k = 1, 长度为1 的推导只有1个，即 S ⇒_G e , 此时生成空串，有0个a 和 b ，符合条件

   2. 归纳假设 , 假设对所有 k <= n 的推导S ⇒_G e , 其生成的字符串w都在L中

   3. 归纳步骤，证明k = n + 1的 情况，S ⇒_G SS. , S ⇒_G aSb , S ⇒_G bSa 生成的字符串都在 w 中

3. 再证，任何在 L 中的字符串 w（即 a, b 数量相等的字符串）都可以被文法 G 生成

   1. 基础情况 |w| = 0

   2. 我们现在必须证明，对于长度为 |x| = k + 2 的字符串 x，如果 x ∈ L，那么 G 也可以生成 x。注：为什么是k+2？因为 a, b 数量相等的字符串长度必须是偶数。我们从偶数 k 跳到下一个偶数 k+2）

   3. Case1: x = awb , 根据我们的假设一定有 S ⇒*_G w (已有条件), 然后应用 S ⇒_G aSb ，可得S ⇒*_G awb = x (Case2类似)

   4. Case3 : x= awa, x 一定能被拆分为 x₁x₂ = (au)(va) 使得 x₁x₂ 是平衡的； 并且x_1,x₂ 长度分别都小于等于k，因此，G 一定能生成x₁x₂ ,应用 S ⇒_G SS 可以证得 (Case4 类似)

3.1.3 要证明一个语言是上下文无关的 (CFL)，你只需要为其构造一个上下文无关文法

1. 𝐿₁ = {𝑤𝑤^𝑅: 𝑤 ∈ {𝑎, 𝑏}^∗}

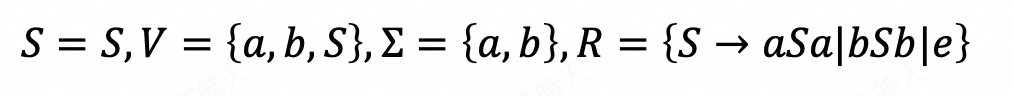2. Show that 𝐿2 = {𝑤 ∈ {𝑎, 𝑏}^∗: 𝑤 = 𝑤^𝑅} is context-free

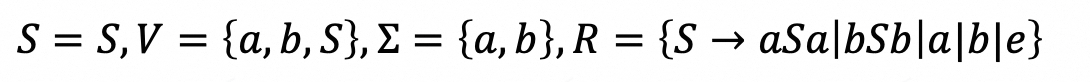(2比1多出来了奇数回文，例如 abbabba)

3.2 Parse Tree

3.2.1 Definition

CFG G = (V, ∑, R, S) 的任何推导都可以用一个语法分析树来表示; 其中，根节点必须是文法的起始符号 (Start Symbol)[例如S]， 叶节点必须是终结符[例如a, b, c]， 内部节点必须是 非终结符 / 变量[例如 S, A, B]

前序 (precedes) 关系的定义；D < D' (D “前序”于 D') 当且仅当1. 除了在某一步 k 附近, 两个推导过程几乎完全相同; 只是在某一步颠倒了两个独立规则的应用顺序。

相似(Similar) 的定义: "D and D' are similar iff (D, D') belong in the reflexive,symmetric,transitive closure of precedes <"

这个定义是理解文法歧义性 (Ambiguity) 的关键; 相似的推导 (Similar derivations)： 它们只是表面上不同（因为你选择先应用哪个独立规则的顺序不同）。它们在结构上是等价的，并对应着完全相同的同一棵“语法分析树”(Parse Tree); 不相似的推导 (Non-similar derivations)： 它们在结构上是根本不同的。它们对应着两棵完全不同的“语法分析树”

每一棵语法分析树都包含一个（在该等价类中）唯一的，在 < 关系（即“前序”关系）下的最大推导或最小推导。

• 一个字符串可以有多个最左推导和最右推导, 因为一个字符串可以由多棵不同的树组成

• 如果两个推导 D 和 D' 有相同的起始符号 x₁ 和相同的最终字符串 xn , 也可能不相似

eg.

“一个文法，如果它生成的语言中某些（至少一个）字符串（单词）对应两棵（或更多）不同的语法分析树，那么这个文法就被称为有歧义的 (ambiguous)。”

3.3 Pushdown Automa

用 FA 无法处理 S → aSa（一个 CFG 规则）这一事实，来证明我们必须引入 PDA（CFL 的识别机器）。

3.3.1 什么是下推自动机 (Pushdown Automata)？

1. 下推自动机 (PDA) 拥有：

   1. 一个输入带 (An input tape)

   2. 一个有限控制器 (A finite control)

   3. 一个栈 (A Stack) <-- 新增的核心组件！

2. PDA 的“动作 (Action)”：

   • 读取： 读一个符号，磁带头右移（或者停在原地，即执行 ε-move）。

   • 思考 (Think)： 这是一个更强大的“思考”过程。

     1. PDA 的决策不仅取决于“当前状态”和“输入符号”，还取决于“栈顶的符号”。

     2. 它的动作不仅是“改变状态”，还包括“操作栈 (manipulate stack)”。

        • Push (压入)： 向栈顶添加新符号。

        • Pop (弹出)： 移除并检查栈顶的符号。

3. 接受条件

   1. 当输入带被读完（为空）、状态是最终状态、并且栈也必须是空的，此时字符串才被“接受”。

3.3.2 PDA 的计算

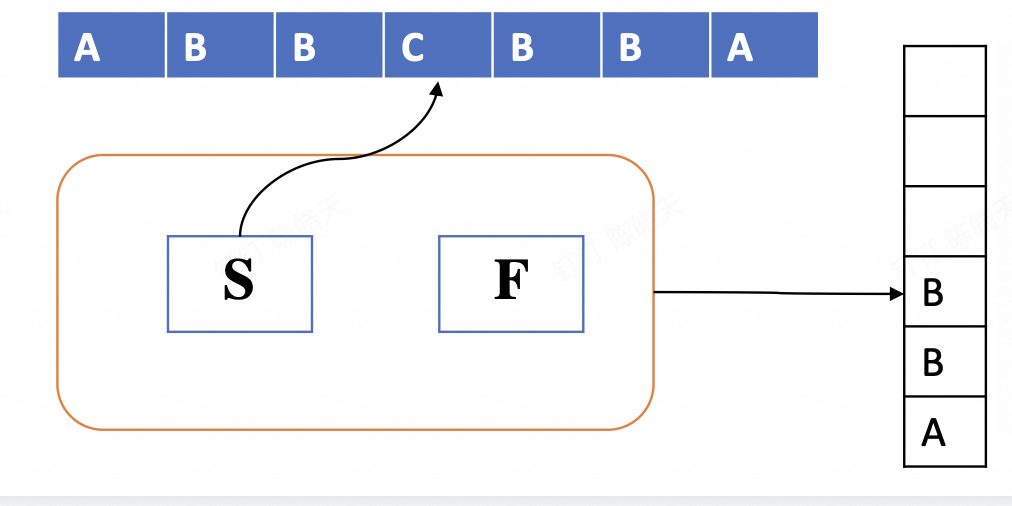
接受 (Accept)： 最终，输入带读完 (e)。

• PDA 停在 f（一个最终状态）。

• 栈是空的 (e)。

• 字符串 "abbcbba" 被接受。

3.3.3 PDA 的形式化定义

一个 PDA 不仅仅是“FA + 栈”，它在数学上被精确定义为一个六元组 (sextuple)，即一个包含六个组件的集合

𝑀 = (𝐾, Σ, Γ, Δ, 𝑠, 𝐹)

• 𝐾 一个有限的状态集合

• Σ 一个字母表 (the input symbols), 和 FA 一样，这是输入带上允许出现的合法符号。

• Γ 一个字母表 这是栈字母表，即允许被压入 (push) 或弹出 (pop) 栈的合法符号。 Γ 可以和 Σ 相同，也可以不同。

• s 起始状态，F 终止状态

• Δ 是一个从 (K, Σ ∪ {e}, Γ*) 到 (K, Γ*) 的映射子集

3.3.3.1 Δ 转移关系的运作方式

1. PDA 转移规则的通用范式 ((p, u, β), (q, γ))

2. 表示机器当前必须处于状态 p ; 机器读取输入符号 u ，从栈顶弹出 (pop) 字符串 β ；然后 机器进入新状态 q，最终机器向栈顶压入 (push) 字符串 γ。

3. 区分 PDA 的两种转移：消耗输入的转移 (读头右移); 不消耗输入的 ε 转移 (读头不动)。

3.3.4 下推状态机的性质

3.3.4.1 为什么下推自动机 (Pushdown Automata, PDA) 本质上是非确定性的 (nondeterministic)。

例如，已知语言 L(M) = {ww^R : w∈{a, b}* }, 我们需要构造一个 PDA M来接受这个语言； Δ 具有规则：

不确定性发生在状态q₀，现在是要读入下一个字符？还是说不读取输入(ε 转移)直接切换状态; 这种猜测即为不确定性

3.3.4.2 PDA 的计算过程

PDA 的格局(configuration)，指的是 K × Σ*× Γ* 集合中的一个成员，也就是在PDA在任一时刻的一个快照，包括 K （当前状态） Σ*（剩余输入） Γ*（当前的栈）

(𝑝, 𝑥, 𝛼) ⊢_𝑀 (𝑞, 𝑦, 𝜁)单步转移, 产生一个新的configuration； ⊢*_𝑀 多步转移

3.3.5 任何上下文无关语言 (CFL) 都可以被一个下推自动机 (PDA) 接受

3.3.5.1 构造算法

1. 状态(K): PDA M 只需要2个状态，p = 起始状态, q = 最终状态

2. 栈字母表 (Γ = V): 既包括终结符（如 a, b, c），也包括非终结符/变量（如 S, A, B）,允许存放所有的文法符号。

3. 转移规则 Δ

   1. 初始化规则 ((p, e, e), (q, S)) ，机器一启动， 立即自动跳转到工作状态 q，并将 CFG 的起始符号 S 压入 (push) 栈顶。

   2. 展开/推导规则：((q, e, A), (q, x)) ，对于 CFG 中的每一条规则，A → x (例如 S → aSb); 如果 PDA 在状态 q，不看输入 (e)，且栈顶符号是一个非终结符 A，那么：机器就弹出 (pop) A，并压入 (push) x ; 这完美地模拟了 CFG 的推导步骤

   3. 匹配规则：((q, a, a), (q, e)) 对于每一个终结符 a, 如果 PDA 在状态 q，读取的输入符号是 a，并且栈顶的符号也必须是 a; 那么，机器就消耗这个输入 a（读头右移），并弹出 (pop) 栈顶的 a

4. 这个 PDA M 模拟了输入字符串的最左推导。

这个算法相当于 ， 在 第二步 展开/推导 的时候 ，就是 利用 pda的不确定性把几乎所有的可能给探索了，然后 在 匹配的时候 利用题目中给的上下文无关语言 进行检查是否接受；这里第二步第三步交错进行

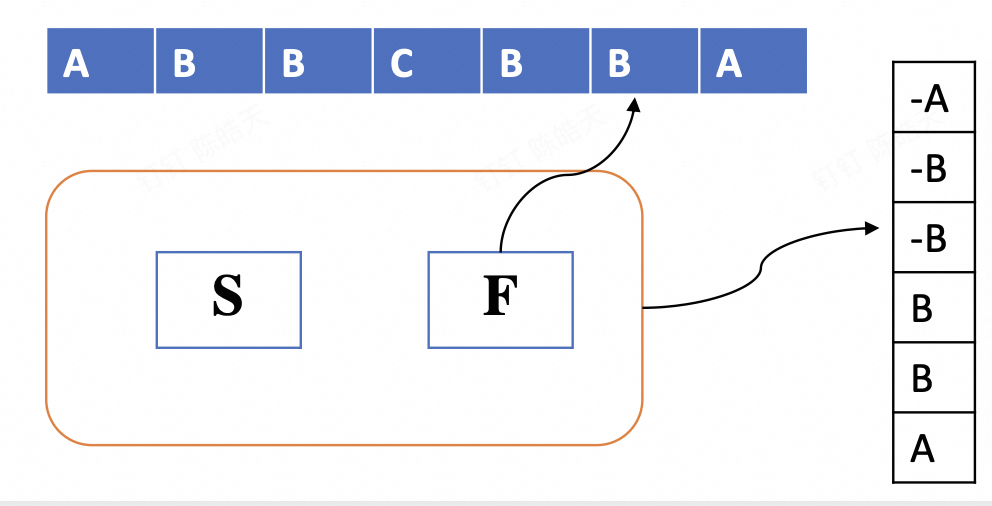
3.3.5.2 具体应用示例

1. 示例: 奇数回文 ; 给定一个 CFG G: 𝑉 = {𝑆, 𝑎, 𝑏, 𝑐}, Σ = {𝑎, 𝑏, 𝑐} , 𝑅 = {𝑆 →𝑎𝑆𝑎, 𝑆 → 𝑏𝑆𝑏, 𝑆 → 𝑐};𝐿(𝐺) = {𝑤𝑐𝑤^𝑅: 𝑤 ∈ {𝑎, 𝑏}^∗}}

2. 构造一个 𝑀 = (𝐾, Σ, 𝑉, Δ, 𝑠, 𝐹) ; 𝐾 = {𝑝, 𝑞}, s = p, F = {q} , 转移规则 Δ 有:

   1. 规则组 I：((p, e, e), (q, S)) (初始化)

   2. 规则组 II：((q, e, S), (q, aSa)), ((q, e, S), (q, bSb)), ((q, e, S), (q, c))

   3. 规则组 III：((q, a, a), (q, e)), ((q, b, b), (q, e)), ((q, c, c), (q, e))

3. ....

4. 最终结果： PDA 停在 q（最终状态），输入带读完 (e)，栈为空 (e)。因此，字符串 "abbcbba" 被成功接受。

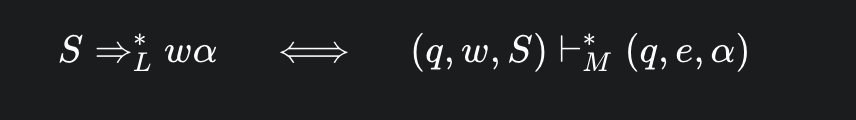
3.3.5.3 证明思路(正向)

1. 需证明 如果文法 G 可以从 S 推出 ωα ，那么 (THEN) 机器 M 就可以在消耗 ω 的同时，把栈从S 变化为 α ;

2. 采用数学归纳法 ； 从0步开始推导，S ⇒_L⁰ , 唯一的结果是 S本身 ，应用于 ωα, 此时ω为空串，α 为 S 本身; 现在我们要证明, (𝑞, 𝑤, 𝑆) ⊢*_𝑀 (𝑞, 𝑒, 𝛼), 代入即 （𝑞, e, 𝑆） ⊢*_𝑀 (𝑞, 𝑒, S）；一个PDA在经过0步计算后，其状态，格局不发生变化，成立

3. 归纳假设: 我们假设“断言”对于所有长度为 n 或更少的 推导都是成立的, 现在证明 n+1 也是成立的

4. 证明方法，构造一个PDA M 来模拟CFG G 的最左推导。

a. 首先分解 n+1 步推导, 变量名阐述

S到u_n是n步最左推导，u_n到u_n+1是第n+1 步推导；ω全为终结符，要么是e，α要么开头是非终结符

设u_n为xAβ的形式，其中 x全为终结符；A是非终结符变量

b. 根据归纳假设(第n步的推导已经被证明可以转化为pda了)，因此有(𝑞, x, 𝑆) ⊢*_𝑀 (𝑞, 𝑒, Aβ),

c. 假设第n步的应用规则是，A → γ , 那么我们有 ε转移: (𝑞, e, Aβ) ⊢*_𝑀 (𝑞, 𝑒, γβ)

d. 定义 y 为 γ的终止符前缀，因此我们有 ω = xy; 因为我们有 ωα = xγβ, 因此 xyα = xγβ , 故yα = γβ

e. 现在我们再证 (𝑞, y, γβ) 能够到达格局 (𝑞, e, α); 由于 γβ 和 yα 等价，因此，只需证 (𝑞, y, yα) 能够到达格局 (𝑞, e, α); 而这和 匹配规则相符（即((q, a, a), (q, e))），所以成立

f. 根据 (b),(𝑞, xy, 𝑆) ⊢*_𝑀 (𝑞, y, Aβ) , 再根据(c), （𝑞, y, Aβ) ⊢*_𝑀 (𝑞, y, γβ) ；再根据(𝑞, y, γβ) ⊢*_𝑀 (𝑞, e, α)，得到(𝑞, ω , S) ⊢*_𝑀 (𝑞, e, α)

举例，永远保持最左推导

3.3.6 如果一个语言可以被 PDA 接受，那么它是一个上下文无关语言 (CFL)

3.3.6.1 证明思路

1. 定义“简单 PDA” 2. 将“任意 PDA”转换为“简单 PDA” 3. 将“简单 PDA”转换为 CFG。

3.3.6.2 如何替换任意PDA为一组等价的、但符合“简单”条件的新规则

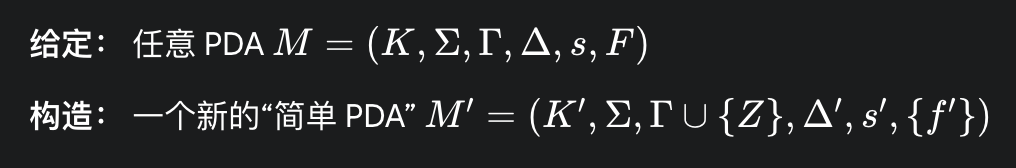
1. 简单PDA的每条转移规则 ((q, α, β), (p, γ))(除了启动规则外，必须满足)

   1. β ∈ Γ 必须且只能从栈顶弹出 (pop) 1 个符号

   2. |γ| ≤ 2 最多只能向栈顶压入 (push) 2 个符号。

   3. 除了转移规则，这个M‘的其他特点

      1. K‘ 新状态集，包含K，再加上两个全新的状态s‘和f’

      2. Γ ∪ {Z} (新栈字母表) , Z 将用作 栈底标记

      3. 新起始状态 s', 和新最终状态集 ，只包含 f'

2. Get rid of transitions with β≥2

   1. 将这个“Pop n”的动作分解成 n 个“Pop 1”的动作。

3. Get rid of transitions with |γ| > 2

   1. 将这个“Push m”的动作分解成 m 个“Push”动作

   2. 注意：压栈 C₁...C_m 意味着 C_m 在最深处，C₁ 在栈顶。所以我们必须倒着压入：先压 C_m，最后压 C₁。

4. Get rid of transitions with β = e (eg. ((q, α, e), (p, γ)))

   1. 将这一条单独的规则删除

   2. 替换为一大组新规则，每种可能的栈符号 A ∈ Γ ∪ {Z} 都有一条 ((q, a, A), (p, γA))，先弹出 A 再压入 γA

3.3.6.3 将简单 PDA M' 转化为 CFG G

1. 目标是构造 上下文无关语法 G = (V, ∑, R, S), 使得G 生成的语言L(G) 与 M' 接受的语言 L(M')完全相同

2. 定义非终结符 (q, A, p)

   1. (q, A, p) 代表所有能被 PDA M' 读入的输入字符串 w 的集合，这些w必须满足以下条件

      1. 计算开始时，PDA 处于状态 q，栈顶是 A。

      2. 计算结束时，PDA 第一次进入状态 p，并且恰好消耗掉了 A 及其在计算过程中产生的所有“子任务”

   2. 最终 V (总变量集)变成了{S} ∪ ∑ ∪ {(q, A, p)| ... }, 其中 S 表示全新的起始符号

3. 定义规则

   1. 起始规则，S → (s, Z, f'), 这是 CFG的唯一入口，表示要解决这个“主问题”： 找到一个输入字符串，能够使得PDA从起始状态s走到最终状态f‘，并且消耗掉整个栈（即消耗掉栈底标记 Z）

   2. “Pop 1, Push 1” 规则 ， PDA 转移： ((q, a, B), (r, C))（其中 a 可为 e， B 和 C 都是单个栈符号）CFG 规则： (q, B, p) → a(r, C, p)（为每一个可能的 p 添加此规则）

   3. “Pop 1, Push 2” 规则

      • PDA 转移： ((q, a, B), (r, C₁C₂))

      • CFG 规则： (q, B, p) → a(r, C₁, p') (p', C₂, p)（为每一个可能的 p 和 p' 添加此规则）[这一步完全在探讨字符串的转化]

      • 这里的 CFG 中几乎只有 a 是和 PDA转移相关的, 彰显了PDA转化，后面的(r, C₁, p') (p', C₂, p) 就是探讨 怎么到 p (p由CFG左侧定义是什么)的，更是一种递归式的长推导，其中黄色标注出来的 p' 完全是 右侧 自定义的，因此可能有好几种组合 ；注意最左边 r 一定是 PDA的 r ， C1 C2 分别 在 CFG规则等式右侧

   4. 终止规则 : PDA 转移： ((q, a, B), (p, e)) 对应的 CFG 规则： (q, B, p) → a

3.3.6.4 示例

转移规则:

如何构造一个PDA:

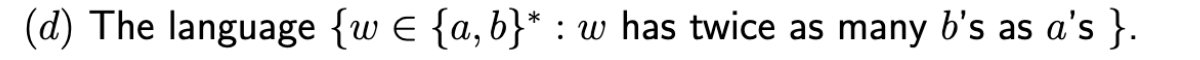
可以看到，F标记为 q 并不意味着状态到了 q 就可以结束，还需要栈为空；因此，构造PDA的时候不需要太考虑繁复的状态关系, 可以通过栈来帮助PDA的构造

3.5 Languages that are and are not CF

3.5.1 Theorem

上下文无关语言 (CFL) 的集合，在并集 (union)、连接 (concatenation) 和克林星号 (Kleene star) 这三种运算下是封闭 (closed) 的。

证明思路： 构造法 ; 我们知道，一个语言是 CFL，当且仅当存在一个上下文无关文法 (CFG) 可以生成它; 所以，要证明这个定理，我们只需要:

1. 假设我们有能生成 L₁ 和 L₂ 的 CFG，即 G₁ 和 G₂。

2. 通过 G₁ 和 G₂，构造出一个新的 CFG (称为 G)。

3. 证明这个新 G 生成的语言 L(G) 恰好等于 L₁ ∪ L₂

重要假设: 我们假设 G₁ 和 G₂ 的非终结符 (变量) 集合是不相交 (disjoint) 的

1. 构造 G 来生成 L(G₁) ∪ L(G₂)。

   1. 新变量： G₁ 的所有变量 ∪ G₂ 的所有变量 ∪ {S} (S 是新起始符号)。

   2. 新规则： G₁ 的所有规则 ∪ G₂ 的所有规则 ∪ {S → S₁ | S → S₂}。

   3. 

2. 构造 G 来生成 L(G₁)L(G₂)

   1. 新变量： G₁ 的所有变量 ∪ G₂ 的所有变量 ∪ {S}。

   2. 新规则： G₁ 的所有规则 ∪ G₂ 的所有规则 ∪ {S → S₁S₂}。

   3. 

3. 克林星号 (Kleene Star)

   1. 新变量： G₁ 的所有变量 ∪ {S}。

   2. 新规则： G₁ 的所有规则 ∪ {S → S₁S | S → e}

3.5.2 The CFL are not closed under intersection or complementation

上下文无关语言 (CFL) 的集合，在交集 (intersection) 或补集 (complementation) 运算下是不封闭 (not closed) 的

换句话说，你可以找到两个上下文无关语言 L₁ 和 L₂，但它们的交集 L₁ ∩ L₂ 不是一个上下文无关语言。

前提提示， 正则语言是在“交集”和“补集”下封闭的。对于交集， 我们通过并行模拟（parallel simulation）两个 DFA（确定性有限自动机）来构造一个新的 DFA；对于补集： 我们通过将一个 DFA 的“接受状态”和“非接受状态”互换来构造。

这两个证明都严重依赖于我们的自动机是确定性的 (deterministic)

CFL 的标准机器模型是非确定性的 (nondeterministic) PDA

反例：

L₁ = {aⁿbⁿcᵐ : m, n ≥ 0}, L₂ = {aᵐbⁿcⁿ : m, n ≥ 0} , L1 L2 都是 CFL

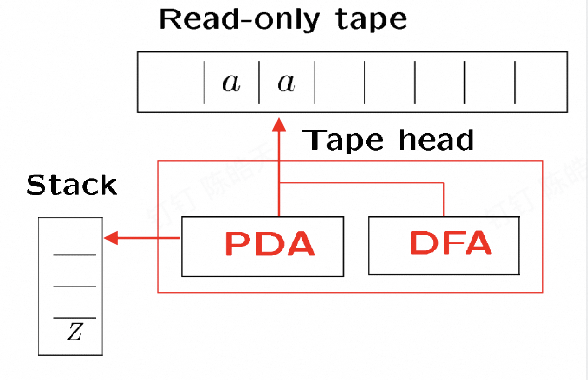
3.5.3 一个上下文无关语言 (CFL) 与一个正则语言的交集 ，必定是一个上下文无关语言 (CFL)

CFL ∩ Regular 意味着我们只需要一个“有栈的机器”(PDA) 和一个“没有栈的机器”(FA) 同时工作。事实证明，PDA 有足够的能力来同时完成这两项任务。

新的机器：

1. 从同一条输入带 (Read-only tape) 读取。

2. 其“大脑”是一个组合体，同时跟踪 PDA 的状态和 DFA 的状态。

3. 它只使用原始 PDA M1 的栈。

4. FA (M2) 的部分完全不操作栈 (do not manipulate Stack)。

3.5.4 Pumping Theorem

定理： 设 G 是一个上下文无关文法 (CFG)。那么存在一个特定的“泵长度” p， 对于 L(G)（G 生成的语言）中任何长度 |w| ≥ p 的字符串 w， w 必定可以被拆分成五个部分 w = uvxyz，并且必须满足以下两个条件、

1. |vy| ≥ 1

2. uvⁿxyⁿz ∈ L(G) (对于所有 n ≥ 0)

3. |𝑣𝑥𝑦| ≤ 𝑝

例子: 证明 L_n= {aⁿbⁿcⁿ : n ≥ 0} 不是一个 CFL

假设 L 是 CFL ； “对手” (AI) 给出“泵长度” p；我们（证明者）选择“陷阱”字符串 w = a^pb^pc^p；我们（证明者）必须证明，无论“对手”如何拆分 w，我们总能获胜（即找到一个 i 使得 uvixyiz∉. L(不属于)）

因此要讨论所有情况, 故分类讨论

1. Case 1: v, y 包含所有三种符号 (a, b, c) ：那么 v，y里至少有一个包含了至少两个符号，这会导致顺序错误

2. Case 2:v, y 只包含两种符号: 这会导致数量不等

3. Case 3: v, y 只包含一种符号: 这会导致数量不等

任何一个仅基于单个字母字母表（例如 = {a}）的上下文无关语言 (CFL)，必定是一个正则语言

例子：证明𝐿 = {𝑤𝑤|𝑤 ∈ {𝑎, 𝑏}*} 不是上下文无关的

考虑到 𝐿1 = {𝑎ⁱ𝑏^j𝑎ⁱ𝑏^j|𝑤 ∈ {𝑎, 𝑏}^∗} （CFL ∩ Regular = CFL）；取字符串𝑎^p𝑏^p𝑎^p𝑏^p 可以用泵定理证明无论如何拆分都会导致矛盾

( 𝐿 = {𝑤𝑤^R|𝑤 ∈ {𝑎, 𝑏}*} 是上下文无关的) (aⁱb^jb^jaⁱ 是上下文无关的，虽然我们可以取这样的字符串 a^pb^2pa^p的分割,但是最终看能不能被接受还是要看在不在 aⁱb^jb^jaⁱ 之中 而不是 a^pb^2pa^p 之中)

例子：证明 𝑳 = {𝒂𝒃^𝒎𝒄^𝒏𝒂^{𝒎+𝟐𝒏}𝒄|𝒎, 𝒏 ≥ 𝟎} 是上下文无关的

证法1: Give a CFG for L

𝑮 = 𝑽, 𝜮, 𝑺, 𝑹 , 𝑽 = 𝑺, 𝑺𝟏, 𝑺𝟐, 𝒂, 𝒃, 𝒄 , 𝜮 = {𝒂, 𝒃, 𝒄}

𝑹 = {𝑺 → 𝒂𝑺_𝟏𝒄, 𝑺_𝟏 → 𝒃𝑺_𝟏𝒂, 𝑺_𝟏 → 𝑺_𝟐, 𝑺_𝟐 → 𝒄𝑺_𝟐𝒂𝒂}

证法2: 其语言都可以通过 PDA 接受

3.5.5 判断以下属于 CFA 吗？

(1)

(2) {𝒂, 𝒃}^∗−𝒂^𝒏𝒃^𝒏

这题的解题方式很奇妙，由于 CFA是关于 减法不封闭的，所以说我们可以将其化为两个 CFA 的并集

可以这样化 : ({𝒂, 𝒃}^∗ 中b都在a后面的字符串 ,且a b数量不等 ) ∪ ({𝒂, 𝒃}^∗ 中存在 b 在 a 前面的那些字符串 )

(3) {𝒂^𝒊𝒃^𝒋𝒄^𝒌: 𝒊 ≠ 𝒋 𝐨𝐫 𝒋 ≠ 𝒌 𝐨𝐫 𝒊 ≠ k } T

只需要创造 三个 CFL 的并集，即a b 数量不相等 的 𝒂^𝒊𝒃^𝒋𝒄^𝒌 ， b c 数量不相等的 ......

(4) {𝒘𝒖𝒘: 𝒘, 𝒖 ∈ 𝚺^∗}

T, L = 𝚺^∗

(5) 上下文无关语言 (Context-Free Languages, CFLs) 不具有子集封闭性 (not closed under subset)

(6) L_a = {a^mbⁿ : m ≠ n}

(7) Use closure under union to show that the following languages are context-free

{a, b}* - L , where L is the language L = {babaabaaab...ba^n-1baⁿb : n ≥ 1}

（注：这里L不是一个 CFL）

这个表达式可以分为两个 CFL 的并集：一个是，不以 ba开头的字符串，或者不以b结尾的，或者有两个连续b存在的，这是第一种情况；第二种情况是这样的形式 : {s = {a,b}* {ba^m}{baⁿ}{a,b}* , n ≠ m + 1} , 这是一个 CFL ；两个取并集就是所需的语言

(8) 证明 a 的 n² 次方不是 CFA 的

由于 a 的 k²次方属于 a 的 n² 次方 ，而 a 的(k+1)² 次方的指数部分 k² + 2k +1 与 k² 相差了 2k + 1, 大于泵长度 k，因此取 vy 的重复次数为2，则会比 k² + 2k +1 长度来的小， 不属于原来的语言

(9) 证明 {aⁿ | n为合数} 不是 CFA

原题

(1) 先应用同态，定义 h(a) = a, h(b) =b

(2) 将这个 h 应用于 L , 得到新语言 L' : L' = h(L) = {aⁿ | n是一个合数} (关键定理: 如果 L 是一个 CFL，那么h(L)也是一个CFL)

(3) 现在我们假设 L' 是一个 CFL ， 由于 L‘是一元语言，因此根据关键定理，任何一元字母上的CFL，必定也是一个正则语言

(4) 如果一个语言是正则的，那么他的补集也是正则的；即 L'_copmliment = {a^p | p是质数} ∪ {a⁰, a¹}}

(5) 而质数之间的间隙是无限的，泵定理也可以得出 {a^p | p质数}不是正则语言

Ch4. Turing Machine

4.1 The Definition of Turing Maching

4.1.1 定义

一个图灵机被定义为一个五元组 (quintuple) : (𝐾, Σ, 𝛿, 𝑠, 𝐻)

1. 𝐾 : 一个有限的状态集合 (a finite set of states)

2. Σ 一个字母表 (an alphabet) 这是图灵机“纸带”上所有允许出现的符号的集合。

   1. 包含 ⊔ (空白符号), ⊳ (左端点符号)

   2. 不包含 → and ← ， 这两个箭头符号是用来描述“动作”的，不能被写在纸带上

3. 𝑠 ∈ 𝐾 初始状态

4. 𝐻 ⊆ 𝐾 停机状态集合 (the set of halting states)

5. 𝛿 转移函数 (𝐾 − 𝐻) × Σ → 𝐾 × (Σ ∪ {← , →})

   1. 定义域为 (𝐾 − 𝐻) × Σ , 表示只有当机器处于一个非停机状态时，才会有规则可循

   2. 输出也是一个二元组 ，（ 下一个状态，要执行的动作），动作可以是:

      1. 在纸带当前格上写入一个新符号（来自 Σ）。

      2. 将读写头向右移动一格 (→)。

      3. 将读写头向左移动一格 (←)。

   3. 另有规则:

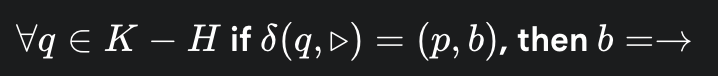      1. 如果机器的读写头在纸带的最左端（读到 ⊳ 符号），那么它执行的动作 b 必须是向右移动

      2. 机器永远不能写入⊳ 符号, ⊳ 只能在纸带最左端出现一次

4.1.2 性质

1. 图灵机是确定性的 , 对于任何一个（状态, 读取符号）的组合，只有唯一的一条路径可走

2. 接受 (Accept) vs 拒绝 (Reject)

   1. Accept Input string : 如果机器最终停机，并且停机时所处的状态是一个接受状态

   2. Reject Input string : 机器停机了，但停机时所处的状态是一个非接受状态 或者 机器永不停止，进入了一个无限循环

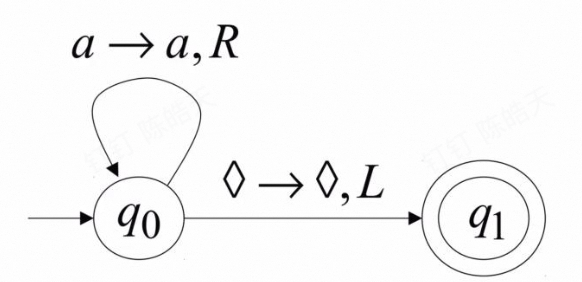
4.1.3 例子

1. Accept the language a*

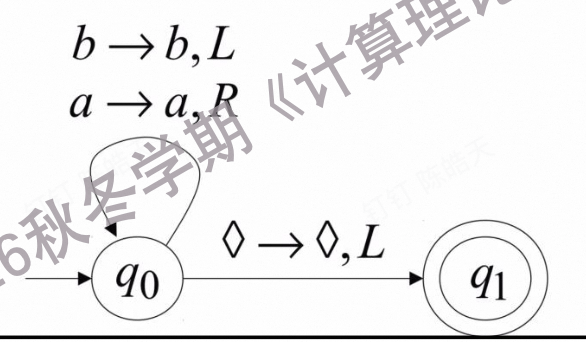
2. Accept the language a* + b(a + b)*

此处如果 输入b的话，直接跳到 ⊔ , 可以直接被接受 (因为一旦开头是b，后面不管是什么，甚至是空，都可以接受)

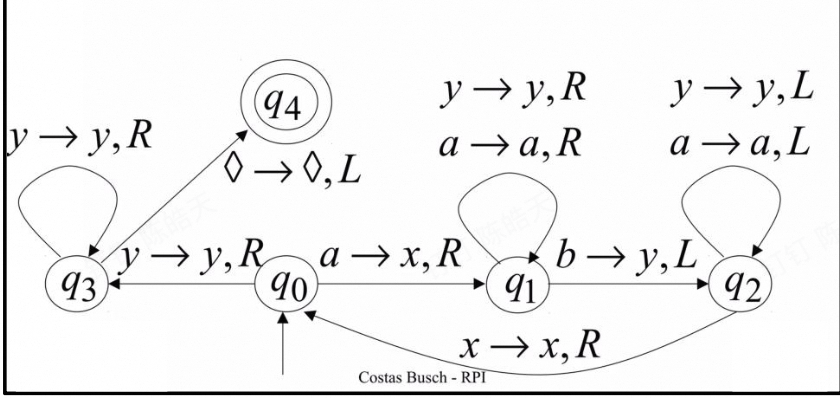
3. Accept the language {aⁿbⁿ}

4.1.4 Turing Machine Configuration

1. 一个完整的配置需要三部分信息，并被表示为一个三元组 (q, ⊳x, y)

2. 假设纸带为 ⊳bbcade⊔ , 则配置为 (q₅,⊳bbca, de)

3. 详细定义 : 𝐾 × ⊳ Σ^∗ × (Σ^∗ (Σ − {⊔} ) ∪ {e}) ; 最右侧字符串 为 y, 表示 y 是一个以非空白符号结尾的字符串，或者是 e

A simplified notation of configuration 简化

（q, wa, u）⇒ (q , wau)

(𝑞₁, 𝑤₁𝑎₁𝑢₁) ⊢_M (𝑞₂, 𝑤₂𝑎₂𝑢₂) , 当且仅当

1. 𝛿(𝑞₁, 𝑎₁) = (q₂, b)

2. 这个 b 必须是 Σ 中的一个符号(写入) , → 和 ← 中的一种

⊢*_M 是 ⊢_M 的自反，传递闭包 ， 这个符号表示在零步或者多步到达

4.2 Computing with Turing Machine

4.2.1 Definition

1. Decide，这是一个比“接受”更强大的定义。

2. 如果说，M 决定 L，那么机器 M 必须能够对任何可能的输入字符串 w 给出明确的 “是”或“否”的答案

𝑀 decides 𝐿 ⊆ Σ∗ if ∀𝑤 ∈ Σ*，the following is true:

𝑤 ∈ 𝐿 iff 𝑀 accepts 𝑤 ; 𝑤 不属于 𝐿 iff 𝑀 rejects 𝑤

3. Recursive

A language 𝐿 is recursive if ∃ a TM that decides 𝐿

(𝐿 = 𝑎^𝑛𝑏^𝑛𝑐^𝑛, 𝑛 ≥ 0 是 递归的)

4. 图灵机 (TM) 是更强大的模型 , 相对于 NFA , PDA , 它有第三种结果：无限循环。它可以通过无限循环来回避回答问题

5. 有可数无限个 递归语言；因为，任何一台图灵机都可以被一段有限长度的字符串来完整描述， 所有可能的字符串的集合是可数无限的，因此，所有可能的图灵机的数量也是可数无限的，因此Deciders也是；而 根据定义，一个语言 L 是“递归的”，当且仅当存在一台（或多台）图灵机 Decider 来决定它，因此 递归语言数量肯定不会多于deciders

6. “不可数”远远大于“可数”。这意味着，在所有可能的语言中，绝大多数的语言是不可决定的 (not recursive / undecidable)。

4.2.2 Recursively Enumerable

4.2.2.1 半判定 (Semidecides)

1. M是图灵机，L是语言，w是输入字符串

2. 图灵机M半判定 语言L，当且仅当 如果w ∈ L，图灵机 M 会停机，如果 w 不属于 L，则图灵机M不会停机

4.2.2.2 递归可枚举语言 (Recursively Enumerable / R.E.)

如果存在一个图灵机 M 能够半判定语言 L，那么语言 L 就被称为递归可枚举语言（R.E.）。

4.2.2.3 如果 L 是递归语言，那么它也是 R.E.

• 假设 L 是递归的，那么存在一个图灵机 M 能判定它（即 M 在状态 y 和 n 都会停机）。

• 我们要构造一个新的图灵机 M' 来半判定 L。

• 改造方法：

  • 如果原机器 M 进入状态 y（接受），新机器 M' 也停机。

  • 如果原机器 M 进入状态 n（拒绝），强行让新机器 M' 进入死循环（永远不停）。

• 这样，新机器 M' 就符合“半判定”的定义了：只有输入在 L 中时才停机，否则死循环。所以 L 也是 R.E. 的。

4.2.2.4 半判定与 R.E. 语言的实例

1. 语言定义: L = {w ∈ {a,b}* , w contains at least one a}.

2. 对应图灵机逻辑: 只要读到的字符不是 a（即读到 b 或者空白），就向右（Right）移动并保持在当前状态。

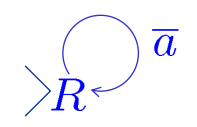
3. 情况 1（字符串里有 a）读到 a 时，不满足循环条件，于是它跳出循环; 在图中隐含的意思是它停机（Halt）情况 2（字符串里没有 a）：比如输入 bbb。机器读 b（向右），读 b（向右）... 读完所有 b 后进入无限的空白带（Blanks）。因为空白也不是 a，机器会永远向右跑下去。

4. 因为这个机器对属于 L 的词停机，对不属于 L 的词不停机，所以它半判定（semidecides）了 L。因此，语言 L 是 递归可枚举的（R.E.）。

5. M(w) = ↑ ; 这个向上的箭头符号在计算理论中专门表示“发散” (diverges)，即不停机

4.2.2.5 递归语言的性质

1. 递归语言补集还是递归语言

既然 L 是递归的，那肯定有一个判定器 M，它对任何输入都会停机。我们可以构造一个新的机器 M'（即 L 的补集机器）。

做法：把 M 的接受状态 (y) 和拒绝状态 (n) 互换。

2. 定理：递归语言的并集/交集还是递归语言

“并行”模拟：图中的气泡提示 "parallel" simulation。这意味着 M₃ 可以同时（或者交替一步步地）运行 M₁ 和 M₂。

对于并集 (Union)：只要 M₁ 或 M₂ 中有一个接受，大机器 M₃ 就接受。

对于交集 (Intersection)：只有 M₁ 和 M₂ 都接受，大机器 M₃ 才接受。

3. 图灵机的用途

   1. 判定语言

   2. 计算函数: 假设图灵机 M 在输入 w 上运行，最终停机；(s, ⊳⊔w) ⊢^∗_M (ℎ, ⊳⊔y ), 磁带上留下y，即M在输入w的输出，记作M(w)

   3. 假设有一个函数 Σ₀^∗ → Σ₀^∗了（从字符串映射到字符串）；如果对于每一个输入 w ,图灵机 M 的输出M(w) 恰好等于 f(w), 则称M计算了f

   4. 如果存在一个图灵机 M 能够计算函数 f，那么函数 f 就被称为递归函数（Recursive Function）

4.2.3 函数计算机应用实例

1. 复制机

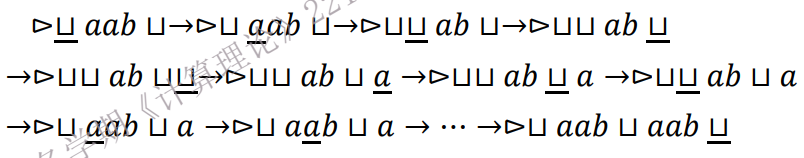
>R : 开始，向右移动找到 w 的第一个字符。循环部分(a ≠ ⊔): 只要当前读到的不是空白（即还在 w 内部），→⊔把当前字符 a 替换成空白（标记）； R²_⊔向右移动，直到跳过两个空白（跳过 w 结尾的空白，到达复制区的空白）; a 在复制区写下字符 a ; L²_⊔向左移动，直到跳过两个空白（回到原字符串区）; a 把原来的空白改回 a（恢复）;然后箭头指回 R，准备处理下一个字符。

2. 左移机

4.2.4 递归函数的定义与实例

1. 定义 f : N^k → N is recursive if ∃ a TM M computes f.

2. 后继函数 (Successor Function)

• 设计一个机器计算 succ(n) = n + 1

• 

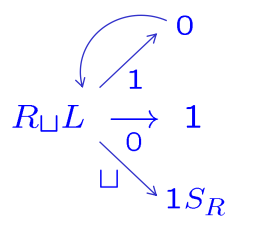
• SR 调用右移机 (Right-shifting machine) 为什么要右移？ 因为标准的磁带格式通常是 ⊳⊔w 。刚才我们在那个 ⊔ 的位置写了 1，导致起始符和数字之间没有空格了。所以需要把整个字符串整体向右挪一格，把那个标准的间隔空格 ⊔ 让出来。

4.2.5 The rules for combining Machines

定义了图灵机世界的 “条件分支语句”. 假设你有三台机器 M1 M2 M3, 先运行 机器 M1, 等 M1 运行结束后，观察 Head正指向字符的什么；如果指的是 a ，则启动机器 M2；如果是 b，则启动机器M3

这个规则赋予了图灵机处理逻辑判断的能力。

4.3 Extension of Turing Machine

这些“增强”并不会增加图灵机的计算能力。凡是多带图灵机能解决的问题，最原始的单带图灵机也能解决

4.3.1 Multiple tapes

1. 定义: K-tape TM 是一个五元组 (𝐾, Σ, 𝛿, 𝑠, 𝐻) , 𝐾, Σ, 𝑠, 𝐻 和普通图灵机一样 , 区别在于 𝛿 : 𝛿 : (K - H) × Σ^k → K × (Σ ∪{← , →})^k; 输入同时读取 k 个符号， 输出 对 k条子带分别执行操作

2. 格局: 𝐾 × （⊳ Σ^∗ × (Σ^∗ (Σ − {⊔} ) ∪ {e}))^k

4.3.1.1 多带图灵机的约定

原始输入字符串只放在第一条带子（First Tape）上;除了第一条，其他所有带子（第 2 到第 k 条）一开始全是空白（Blank）的计算结束时，我们只看第一条带子上的内容作为输出结果

1. 如何用 2-带图灵机 实现字符串复制功能:

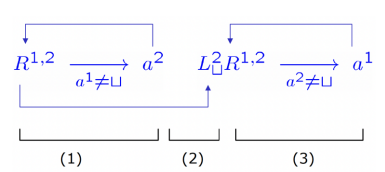阶段 (1)：备份 ; 两个读写头同时向右移动 (R^1,2) 只要带子 1 读到的不是空白, 就把这个字符 a 抄写到带子 2 上;

阶段 (2)：倒带 ; 带子 2 的读写头向左跑 直到回到开头（遇到空白）

阶段 (3)：粘贴 两个读写头同时向右移动 现在开始读取带子 2 上的内容 把它写到带子 1 当前的位置上(a¹)

2. 任意二进制数加法

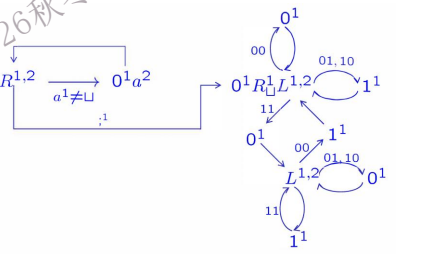
• 左边的部分(R^1,2) 是“抄写”阶段，把第一个数搬到带子 2

• 右边的复杂部分：是“加法”阶段

  • 上面的圈 (State 0)：表示当前无进位 (Carry = 0)

  • 下面的圈 (State 1)：表示当前有进位 (Carry = 1)

4.3.1.2 k-tape TM/Standard TM Equivalence

任何一个 k-带图灵机 (M)，都存在一个标准图灵机 (M') 能够模拟它

• 时间复杂度: 如果M运行了t步，那么 M' 大约要运行 O(t(|x|+t)) 步 ,简记为 O(t²)

• 如果你只有一条纸带，通过什么步骤才能假装自己有 k 条纸带？

  • 把输入的字符串 w 整体向右移一格 ; 在空出来的第一个格子上，写上符号 (⊔, 1, ⊔, 1, ... , ⊔, 1) 共k组；表示所有 k 个虚拟读写头（Head）目前都停在这里

  • 对于输入 w 的每一个字符 a，把它改写成 (a, 0, ⊔, 0, ..., ⊔, 0)，共k组

4.3.1.3 Multiple Heads

这种机器只有一条纸带（One tape），但是有多个读写头（Several heads）在每一步操作中，所有的读写头会同时感知它们各自当前所在的符号，并且独立地进行移动或写入操作。

多头图灵机的计算能力并没有比标准图灵机更强

为了用标准图灵机（或单头机器）模拟多头机器，我们需要解决“如何在一个带子上记录多个头的位置”的问题

1. 将纸带（Tape）在逻辑上划分成多条“轨道”; 其中一条轨道用来存储原本的数据符号, 其他的轨道用来标记各个“读写头”的位置

2. 两遍扫描. 第一遍扫描： 找到所有读写头当前所在位置的符号（以此决定下一步做什么）; 第二遍扫描： 根据规则，去更新那些符号，或者移动那些代表“读写头”的标记

4.3.1.4 Two Dimensional Tape

4.4 Nondeterministic Turing Machines

4.4.1 Definition

1. 非确定性图灵机 (NTM) 也是一个五元组 M = (𝐾, Σ, Δ, 𝑠, 𝐻) , 其他四个和标准图灵机完全一样，区别在于 Δ

2. Δ 是一个关系，是原集合的一个子集, 这个原集合是 （（K − H) × Σ ) × ( K × ( Σ ∪ {←, →} ) )

4.4.2 NTM semidecides Languages

1. 什么是“接受”？

至少有一条路径（at least one branch）最终进入了停机状态（h∈ H），我们就说这台机器接受 (accepts) 了这个输入

2. 半判定

如果一个语言 L 中的每一个字符串 w，都能被 NTM M 接受， 那么就说 M 半判定了语言 L。

4.4.3 NTM decides Languages/Computes Functions

4.4.3.1 NTM 判定语言 (Decides a Language)

• 要求 NTM 必须在有限步内给出答案，不能死循环

1. 条件1，必须停机，即存在一个足够大的N，使得没有这样一个configuration C (s, ⊳⊔w) ⊢^N_M C ； 即经过足够大的推导步骤，肯定都会到达停机的configuration，不会有进一步的推理使得能够到达下一个configuration了

2. 条件2， w ∈ L if and only if , (s, ⊳⊔w) ⊢^*_M (y, uav) for some u, v ∈ Σ^∗ , a ∈ Σ. 如果是 L 的成员（Yes）：至少有一条路径停在接受状态 y ; 如果不是 L 的成员（No）：由于条件 1 保证了所有路径都会停机，且根据逻辑（if and only if），这意味着所有路径都必须停在拒绝状态 n。

4.4.3.2 NTM 计算函数 (Computes a Function)

1. 条件1 ，必须停机

2. 条件2 ， 输出的一致性 (s, ⊳⊔w) ⊢^*_M (h, uav) if and only if 𝑢𝑎 =⊳⊔, and v = f(w); 凡是能停在正确格式 h 的路径，其纸带上的内容 v 必须等于 f(w)

4.4.3.3 非确定性图灵机 (NTM) 应用实例：半判定合数集

合数是指那些除了 1 和它本身以外，还能被其他整数整除的数。NTM 使用非确定性来直接“猜”答案: 机器“猜”两个二进制数 p 和 q, 分裂出无数个并行分支，计算 p*q == n , 如果相等则猜对了，如果不相等则永远继续运行/死循环

合数集实际上是可判定的， 我们可以设置 p,q 小于n，由于可能的 (p, q)组合是有限的，因此NTM计算树会变得有限；如果不相等，我们不让它死循环，而是让它停机并拒绝。这样，如果所有分支都拒绝，机器就输出“No”；如果有分支接受，输出“Yes”。这就变成了“判定”。

4.4.4 非确定性图灵机（NTM）与标准确定性图灵机（DTM）在计算能力上是等价的

NTM 的计算树可能有无数个分支，而且某些错误的分支可能是无限长的; 如果 M’ 采用“深度优先搜索”（DFS），可能会掉进一个无限循环的深坑里出不来；因此应该使用广度优先搜索，先模拟 M 的所有可能的第一步，再模拟第二步，第三步，这种方法保证了覆盖性

如何构造这样一台模拟NTM的标准图灵机 M‘ ？ 我们使用三带图灵机

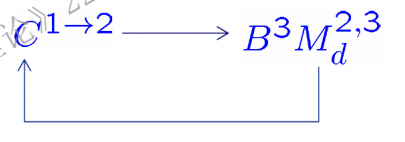
这是一个无限循环的过程，直到找到答案为止. 第一条带始终存放着原始的输入字符串w, 因为我们需要尝试无数条路径，每试完一条失败的路，我们都得“读档重来”. 第二条带 用于模拟 NTM 的实际计算过程. 第三条带 存放着当前的“路径地址码”

C^1→2把第一条带上的原始输入拷贝到第二条带，B³在第三条带上生成字典序的下一个序列，比如上次试了路径 (1,1)，这次就试 (1,2)。M^2,3_d 是一台确定性的机器, 读取第二条带（当前模拟状态）和第三条带（导航指令）, 在第二条带上模拟 NTM 的操作。

为什么逻辑上行为是等价的？因为 M’停机当且仅当M停机

这种模拟带来的时间消耗是指数级增长的

4.5 Grammars

原本的CFG形如这样：A → v ，左边只能是一个 单独的非终结符，并且是上下文无关的，因为我们不关心 A 的左边和右边是什么。

现在，无限制文法有 AXY → AYX ， 其中A就是上下文

4.5.1 Definition

1. G = (V, ∑, R, S)

2. R是规则集，形式为 u → v ， u∈V*(V - ∑)V* , 至少包含一个非终结符 , v∈V*

3. 语言L(G)的定义: 从起始符号S开始 ，经过任意步推导 ⇒*_G 最终生成的只有终结符组成的字符串 w

• 经典例子：L = {aⁿbⁿcⁿ : n≥1}

  • 阶段1: 生成， S → ABCS , S → T_c (最终生成 (ABC)ⁿT_c)

  • 阶段2: 排序， BA→AB, CB→BC, CA→AC (最终AⁿBⁿCⁿT_c)

  • 阶段3：转换

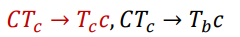
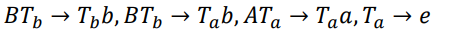
4.5.2 文法（Grammar）与图灵机（Turing Machine）在表达能力上是等价的

4.5.2.1 凡是由文法生成的语言，都是递归可枚举的

我们现在已知一个文法G，现在的任务是构造一个 NDTM，使得 M 能够识别同样的语言

设计一台拥有两条纸带的 非确定性图灵机，第一条带存放原始输入w， 第二条带用来模拟文法的推导过程，一开始第二条带上有起始符号S。

这台机器 M 的运行过程就是一个不断的循环。假设文法 G 共有 |R| 条规则，那么在每一步，机器都有 |R| + 1 种非确定性的选择

1. 选择 1 到 |R| : 应用规则，选一条规则，并且选择一个应用的位置，模拟文法中 w_i ⇒_G w_i+1

2. 或者选择 第 |R| + 1 条规则，检查结果，如果第二条带和第一条带的字符串一样， 则机器停机并接受 ； 如果不相等，继续回到循环，进行下一步推导

4.5.2.2 如果一个语言是递归可枚举的（r.e.），那么它一定可以由一个文法生成

1. 图灵机M的计算方式是，先输入字符串，然后计算，最后停机接受；而文法G的工作方式为，通过起始符号S，经过推导最终生成字符串w。为了等价，我们得让G模仿图灵机的运作，但是方向是反的

2. 为了简化证明，我们让图灵机从 (s, ⊳⊔w)开始，并且假设M如果最终接受并停机，他会清空带子并留下最简单的 (h, ⊳⊔)

3. 为了用文法规则来处理图灵机的状态，我们需要把图灵机的“快照”（格局）写成一个线性的字符串. 假设 Configuration 是(q, ⊳uaw) , 那么对应的string为▷uaqw◁

4. 文法G的规则分为三类：启动、逆向模拟、清理

• 启动规则 𝑆 →⊳⊔ ℎ ⊲

  • 我们假设图灵机如果接受，总是停在最干净的状态 (h, ▷⊔) ， 所以文法的第一步就是生成这个最终结局

• 逆向模拟规则

  • 1. 原地修改： 若TM指令是 (q, a) = (p, b) , 那么有文法规则 𝑏𝑝 → 𝑎𝑞

  • 2. 向右移动 ： 若TM指令是 (𝑞, 𝑎) = (𝑝, →), 那么有𝑎𝑏𝑝 → 𝑎𝑞𝑏

  • 3. 向左移动： 若TM指令是 (𝑞, 𝑎) = (𝑝, ←), 那么有 𝑝𝑎𝑏 → aqb

• 清理规则： ⊳⊔ 𝑠 → 𝑒, ⊲→ 𝑒

4.5.3 Recursive Functions And Recursive Languages

1. 递归函数：一个函数f被称为是递归的（或可计算的），如果存在一个图灵机M，对于任何输入x，图灵机都能停机，并且在有限步骤那输出正确的f(x)

2. 递归语言：一个语言L是递归的（或可判定的decidable），如果存在一个图灵机M，对于任何输入字符串w，都能停机并判断 w 是否属于L

• 递归可枚举语言的话可能会在 w 不属于 L 的时候陷入死循环，因此 递归语言是 递归可枚举语言的真子集

4.7 Numerical Function

4.7.1 Primitive recursive function

• 基础函数

1. 零函数 (The Zero Function) : 𝑍() = 0 或者 zero_k(n₁,...n_k) = 0

2. 后继函数 (The Successor Function) : S(n) = n + 1

3. 投影函数 (The Projection Functions) : P^k_i (x₁, ... , x_n) = x_i ，好比“选择参数”

• 组合与递归

1. 组合 (Composition) ：如果有一个k元函数g (接受k个函数)，和k个l元函数h1, ... , hk , 那么构造 𝑓(𝑛₁, … ,𝑛_𝑙) = 𝑔(ℎ₁(𝑛₁, … , 𝑛_𝑙), … , ℎ_𝑘(𝑛_1, … , 𝑛_𝑙))

2. 递归 (Recursive / Primitive Recursion) : let 𝑔 be a 𝑘-ary function, and let ℎ be a (𝑘 + 2)-ary function

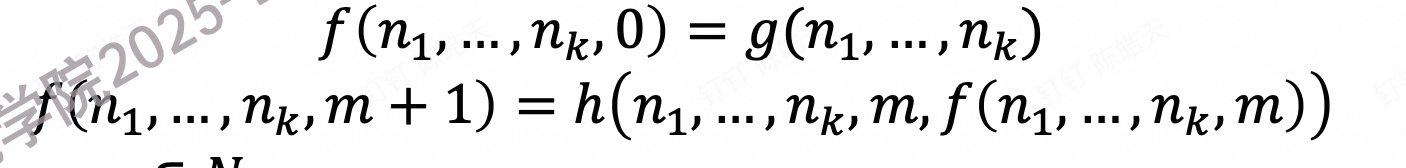
4.7.1.1 定义

原始递归函数是指满足以下条件的所有函数:

1. 它们是基础函数（零函数、后继函数、投影函数）。

2. 或者是通过有限次应用组合和递归操作从基础函数构造出来的。

4.7.1.2 例子(以下都是原始递归函数)

1. plus(m, n) = m + n

plus(m, 0) = m ; plus(m,n+ 1) = succ(plus(m,n))

2. mult(m, n) = m ·n

mult(m, 0) = zero(m)

mult(m,n+ 1) =plus(m,mult(m,n))

3. exp(𝑚, 𝑛) = mⁿ

exp(m, 0) = succ(zero(m))

exp(m,n+ 1) = mult(m,exp(m,n))

4.7.1.3 利用原始递归函数来构建 常数、减法以及逻辑判断（谓词）

1. 常数函数 𝑓 (𝑛₁, … , 𝑛_𝑘) = 𝑠𝑢𝑐𝑐 (… 𝑠𝑢𝑐𝑐 (𝑧𝑒𝑟𝑜 (𝑛₁, … , 𝑛_𝑘)) … )

2. 符号函数 sgn(0) = 0, and sgn(n + 1) = 1

3. 截断减法 ：

• 先定义前驱函数 pred(0) = 0 ， pred(n + 1) = n

• 再定义减法: m ~ 0 = m , m ~ (n + 1) = pred(m ~ n)

4.7.1.4 原始递归谓词 (Primitive Recursive Predicates)

• 一个原始递归谓词就是一个只返回 0 或 1 的原始递归函数。

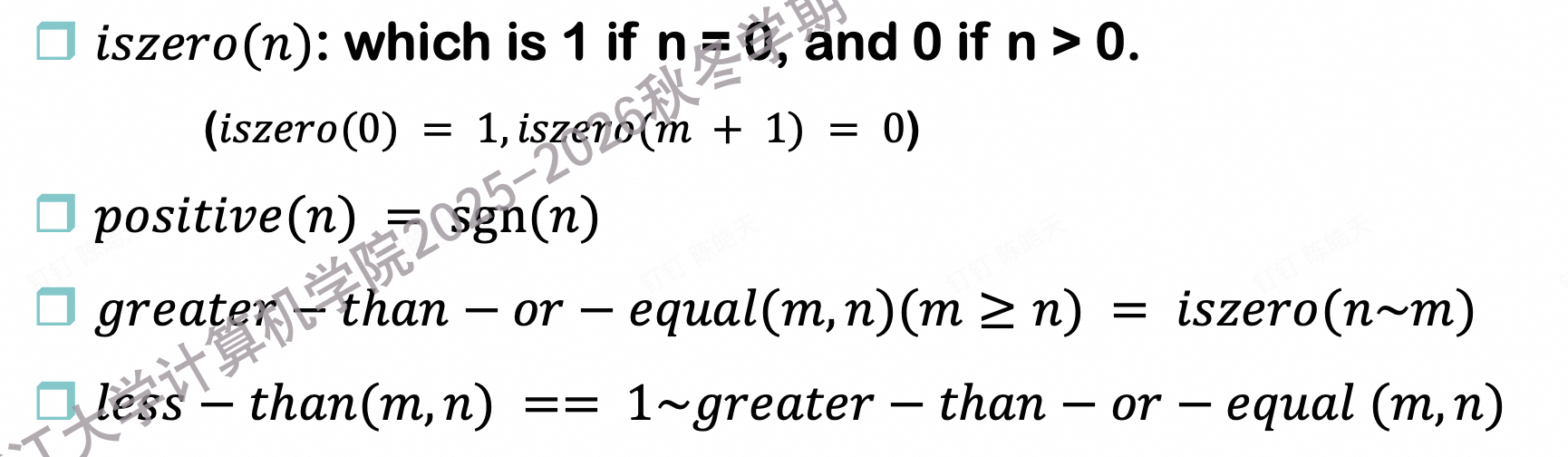
4.7.1.5 原始递归函数模拟布尔逻辑运算

1. 逻辑非: ¬𝑝(𝑚) = 1 ∼ p(m)

2. 𝑝(𝑚, 𝑛) ∨ 𝑞(𝑚, 𝑛) = 1 ∼ 𝑖𝑠𝑧𝑒𝑟𝑜(𝑝(𝑚, 𝑛) + 𝑞(𝑚, 𝑛))

3. 𝑝(𝑚, 𝑛) ∧ 𝑞(𝑚, 𝑛) = 1 ∼ 𝑖𝑠𝑧𝑒𝑟𝑜(𝑝(𝑚, 𝑛) ⋅ 𝑞(𝑚, 𝑛))

4.7.1.6 原始递归函数模拟逻辑控制流

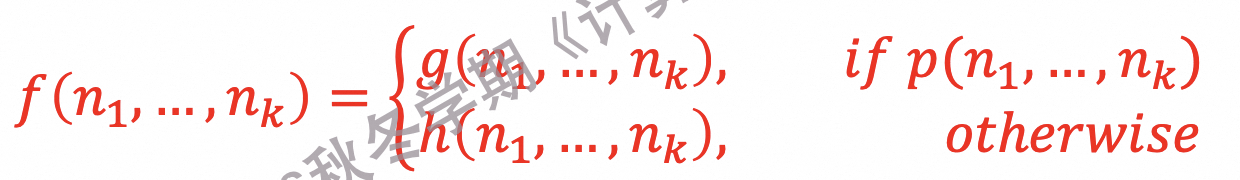
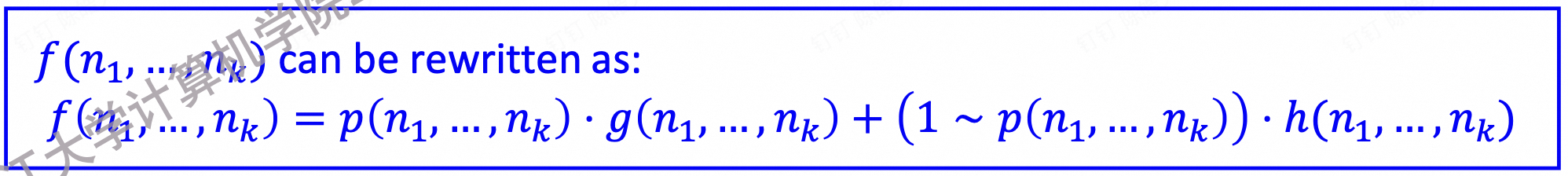
4.7.1.7 定义整除和取余 (div and rem)

1. 取余数

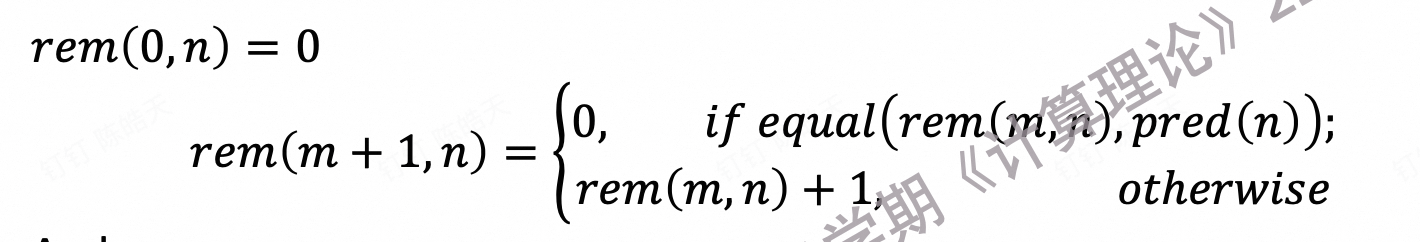
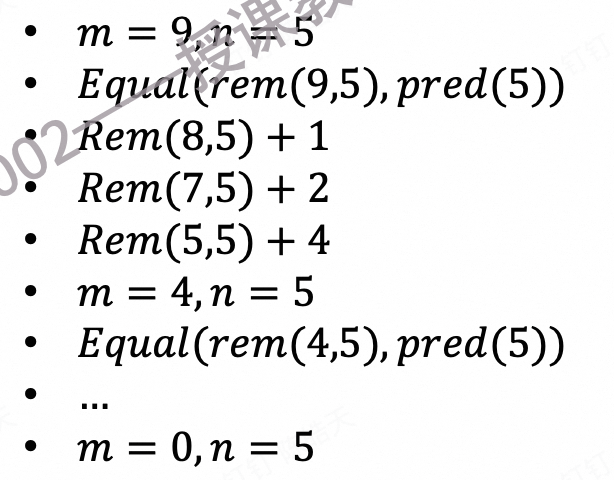
2. 整除

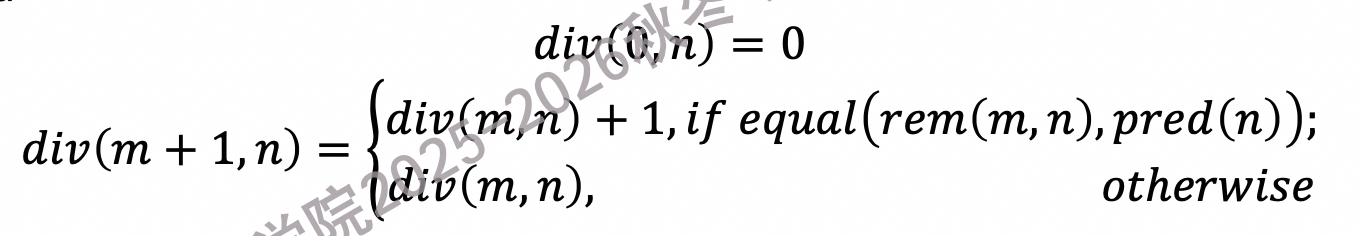
4.7.1.8 数字位提取

目标：digit(m, n, p); 找出数字 n 在 p 进制表示下的第 m 位（从右往左数）

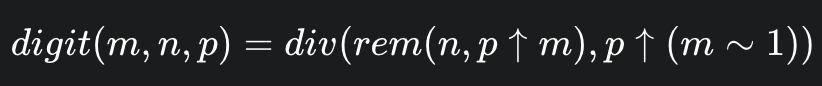4.7.1.9 有界量词 (Bounded Quantifiers)

A. 有界存在量词 ∃𝑡_(≤𝑚), 即，在 0 到 m 的范围内，是否存在至少一个t，使得p(t) 为真？

B. 有界全称量词 ∀𝑡_(≤𝑚), 即， 在 0 到 m 的范围内，是否所有的t，都使得p(t) 为真？

4.7.1.10 整除与素数判定 (Divisibility & Primes)

1. 整除判定 (y|x)

2. 素数判定 (prime(x))

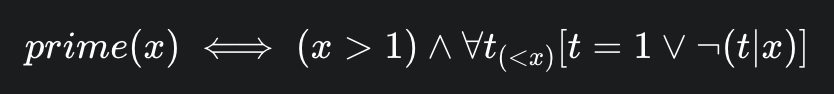
4.7.1.11 原始递归函数是可枚举的 (Enumerability)

1. 原始递归函数的集合是可枚举的 (enumerable)。这意味着我们可以按照某种顺序列出所有可能的原始递归函数

2. 证明逻辑：任何一个原始递归函数，归根结底都是由基础函数（0, S, P）通过有限次的组合和递归操作定义出来的。因此，每一个函数都可以写成一个由有限符号组成的“字符串”或“代码”。既然函数就是字符串，而所有有限长度的字符串是可以按长度顺序一一列举的（就像字典一样）。我们只需要列举出所有字符串，然后筛选出那些符合语法规则的函数定义即可。

4.7.1.12 原始递归的局限性

原始递归函数不能包含所有的可计算函数。

我们之前证明了原始递归函数是可枚举的。也就是说，我们可以把所有的原始递归函数列成一张表 ： f₁, f₂, f₃, ...

我们定义一个新的函数 g(n) = f_n(n) + 1 , 这个 g(n)显然是可计算的

原始递归函数集合是递归函数集合的真子集 (Proper Subset)。

4.7.2 极小化算子 (Minimalization)

1. 定义，给定一个函数 g(n1, ... ,nk, m), 我们定义一个新函数 f 为，找到最小的 m ，使得g(..., m) = 1. 记作 μm[g(n₁, ... , n_k, m) = 1]

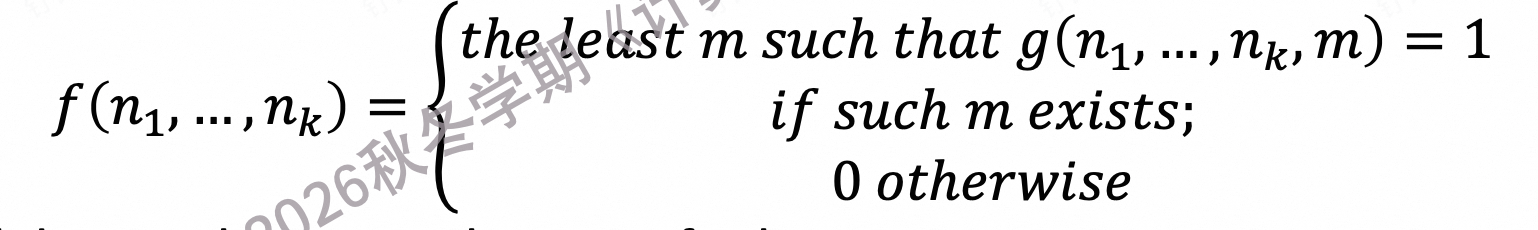
4.7.2.2 极小化算子的可停机问题

在寻找 g(... , m) = 1 中最小的 m 时，逻辑上是一个while循环；但这个循环有可能永远不会停止，在计算机科学的严格定义中，一个“算法（Algorithm）”必须保证在有限步骤内结束。

我们引入“可极小化 (minimalizable)” 的概念，一个函数 g 被称为是可极小化的，当且仅当上述的 while 循环总是能停机

4.7.2.3 μ-递归函数

一个函数被称为 μ-递归函数, 如果它是由基础函数（零、后继、投影）开始，通过有限次的组合、递归定义以及对可极小化函数的极小化操作得到的

对数函数的具体构造

• 通过使用 m+2 作为底数，确保了底数至少是 2。这样就避免了底数为 0 或 1 导致的死循环或无效计算。

• 真数修正 (n+1)：通过使用 n+1，确保了我们要比较的目标至少是 1。

• 可极小化 (Minimalizable)

  • 因为底数 m+2 >= 2，随着指数 p 的增加，(m+2)^p 会迅速增长并趋向无穷大。因此，无论 n 有多大，总是存在某个 p 能让不等式成立。这保证了搜索一定会停机，计算结果总是存在的。

4.7.3 一个函数 f : N^k → N 是 μ-递归 的，当且仅当它是递归的（可被图灵机计算的）

4.7.3.1 如果 f 是 μ-递归 的，那么他一定能被图灵机计算

1. 我们知道基础函数（零、后继、投影）都是很容易用图灵机实现的。

2. 构造 μ-递归函数所用的操作（组合、递归定义、极小化）也都可以被图灵机模拟：

• “组合”就是把一个图灵机的输出接到另一个的输入。

• “递归”就是图灵机的循环或堆栈调用。

• “极小化”就是一个无限循环搜索（Search Loop）。

4.7.3.2 如果图灵机M计算函数 f ， 那么f是 μ-递归的

为了把图灵机的机械动作转化为纯数学公式，证明过程分为三个关键步骤：编码、模拟计算历史、解码结果。

• 确认进制b, 令b等于图灵机的字母表大小加上状态集大小, 这样，每一个字符和每一个状态都可以映射为一个唯一的数字 {0, 1, ... , b-1}

• 多项式编码 : 一个格局 (q, a₁,... a_k ... a_n) 包含了带子上的内容和当前的读写头位置/状态。我们把它看作一串 b 进制的数字序列：a₁...a_k q ...a_n（注意状态 q 插在当前字符旁边）。

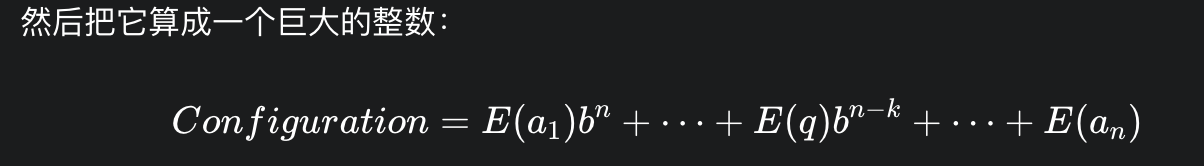
• 图灵机的任何时刻的状态，现在都只是一个巨大的整数了

2. 模拟过程

我们需要构造一个函数，把数字n变成最终输出结果 f(n),公式如下:

f(n) = num(output(last(comp(n))))

• comp(n) : 寻找计算历史. 目标是找到一个数字 m ，这个m编码了图灵机从输入 n开始到停机为止的整个计算过程（所有的步骤序列）

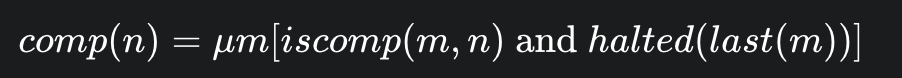
解释：我们使用 μ算子 去搜索一个数字m

iscomp(m, n)：这是一个原始递归谓词，用来检查 m 是否代表一个合法的、从输入 n 开始的计算历史。它会检查序列中每一步是否都符合图灵机的转移函数

halted(last(m))：检查这个历史的最后一步是否处于停机状态 h

• last(n)：提取最终状态 ; comp(n) 找到了整个历史（一长串格局），我们只需要最后那个结果; last 函数从代表序列的数字中提取出最后一个格局

• output(n)：清理磁带 ; 最后的格局里包含了很多杂质：边界符 、空格 、停机状态; 我们只需要 保留带子上代表结果的 0 和 1 的字符串（编码形式）

• num(n)：解码为数字 ； 现在的带子上是一串二进制字符的编码。num 函数把这串二进制编码解释回我们最终需要的自然数结果。