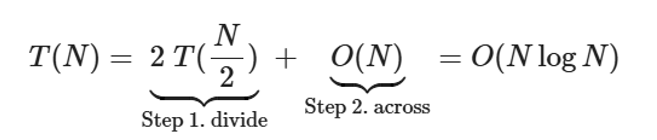写在前面
高级数据结构与算法分析 学习回顾
在上课之前可以对着ppt简单看一遍(或者看一遍线上课,链接 1.1 AVL Trees-教育-高清完整正版视频在线观看-优酷 ),遇到不会的问gpt就行。如果完全不预习的话很可能会跟不上,特别是对于后半学期算法的内容;其实不建议上课翘课课后补智云,因为老师上课提到的很多细枝末节都可能成为考试点;
大部分老师的作业题答案有学长总结过了 Homework - Jianjun Zhou's Notebook,下面的内容可能会有引用
考前2周就可以开始复习了,我的复习方法是先大致看一遍前人的笔记 (nought前辈的笔记 高级数据结构与算法分析 - NoughtQ的笔记本 ;以及这一份 ZJU_ADS/ADS笔记.pdf at main · yile-liu/ZJU_ADS)然后开始做一份历年卷,做到陌生的题的话就再把那个章节对应的自己的笔记以及ppt看一遍;个人认为练习可以很有效地帮助效记忆。大概把这一份历年卷边复习边做完之后,就可以开始完整地按照考试时间刷其他若干份历年卷了。
最终的编程题很可能是DP(动态规划),平时可以多做几道哈。以下是我们考试的DP题目与我的解答。
R6-1 Knapsack - 浙江大学2024-25学年秋冬学期《高级数据结构与算法分析》课程期末考试试卷.html
接下来是我的错题集和易错点笔记 (适合复习完之后查漏补缺,而不是作为完整看ppt的替代品)
如有错误请联系qq1051292989 ,感谢
lecture1 AVL & Splay Tree
1)对于高度为0,1,2,3.....的平衡树 ,需要最少的节点为 1,2,4,7;根据公式 f(n)=f(n-1)+f(n-2)
2) Splaying操作 不仅将被访问的节点移动到根节点,而且将路径上大多数节点的深度大致减半。
3) 在伸展树中,删除一个节点的操作 最多需要两次splay
a. 将要删除的节点 splay 到根节点
b.将左子树的最大节点splay到左子树的根节点(右子树同理)
c.将根节点删掉,右子树接在左子树的根节点右(右边同理)
4) 均摊分析a

5)均摊分析b
新的势能函数 Φ′ 可以定义为:Φ′(Di)=Φ(Di)−Φ(D0)

6) ⭐判断哪个均摊分析是正确的 (important!)
鱼肆周报 002 - 势能分析法 这个比我讲的好,推荐看下
为什么均摊复杂度是对的?
因为均摊分析要求 ϕ(Sn)−ϕ(S0)≥0 这就保证了Σamortized(T)≥Σactual(T),因此如果均摊分析的整体复杂度能降到某个值以下,那么实际的复杂度不会比这个值更高
下图是我们的一道期中题目,他需要保证每个操作的均摊复杂度都为 O(1);我们先去找那个耗费复杂度最高的操作,其复杂度包括迁移原先size(T)个数据,以及插入一个新数据的时间,即 size(T)+1,这不是常数时间的;通过 公式 amortized(T)=actual(T)+ϕ(Sn)−ϕ(Sn-1) ,我们知道虽然 actual(T) 是非常数时间时间复杂度的,但amortized(T)可以是常数的。
分析选项C , 对于那一种耗费复杂度最高的情况, ϕ(Sn-1)=1.25(size(T)−size(T)/5) =size(T) ; ϕ(Sn)=-1.25
因此 amortized(T)=actual(T)+ϕ(Sn)−ϕ(Sn-1) = -0.25, 是常数时间的,可以接受
然后再按这个方法 , 检验一下 某一次低耗费的插入 ,发现没有问题,所以选C
其他几个选项应该都是在那一种耗费复杂度最高的情况下,没有将均摊复杂度将为常数
Lecture2 Red Black Tree & B+ Tree
1) 比较重要的结论,摘自 Lecture 2 | Red Black Tree & B+ Tree - Jiepeng's notes
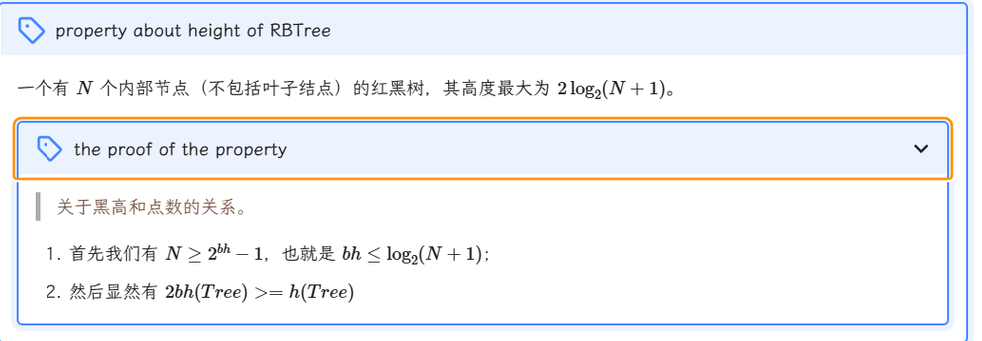
2)红黑树的查找,插入和删除操作,时间复杂度都是O(logN)
3) 红黑树保证最长路径不超过最短路径的二倍
4)For red-black trees, the total cost of rebalancing for m consecutive insertions in a tree of n nodes is O(n+m).
也就是说每个重平衡操作的均摊复杂度是O(1)
5)叶子节点的黑高相同,指的是nil节点
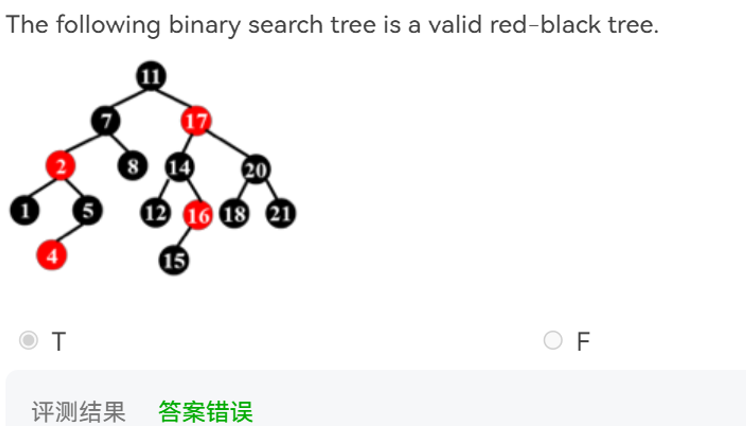
16的右儿子nil的黑高小于15的儿子的黑高,所以不是红黑树
6)B+树给定某个数量的叶子节点,求最多的非叶子节点的数量

方法:自下而上按两个节点共享一个父节点的方法;如果某一层余下了一个节点,则与旁边的两个节点共享一个父节点。
本到底呈现出 1-3-6-12 (数字代表某一层的节点个数)的结构
7)B+树所有叶子节点的高度相同,这一点可以和红黑树的黑高对应起来
8)一些重要结论

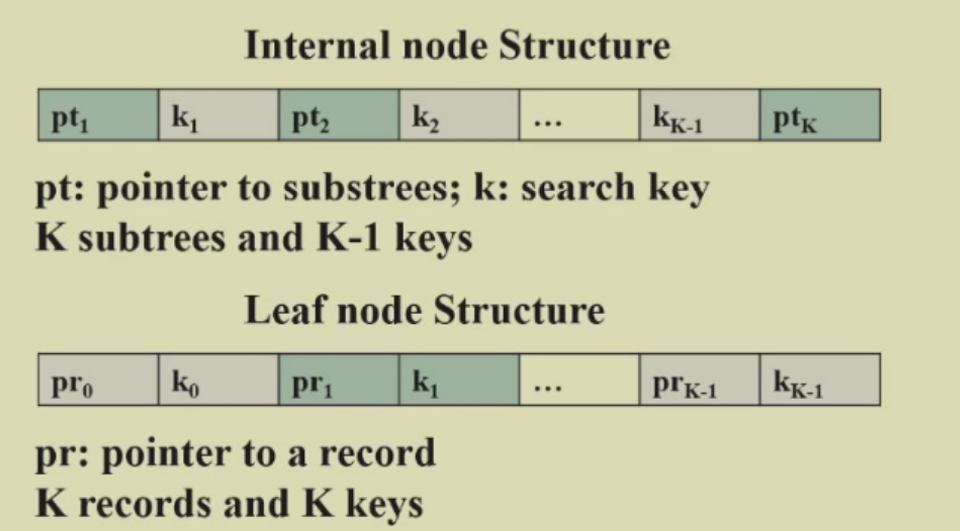
B+树最大的深度
原因:在 B+ 树的每个节点中,元素的数量并不会总是接近满的。在最坏情况下,B+ 树中的节点元素数目可能接近其最小值,而这个最小值为 𝑀/2。因此,为了估算树的深度,考虑的是节点可能最少包含的元素数,即 𝑀/2。
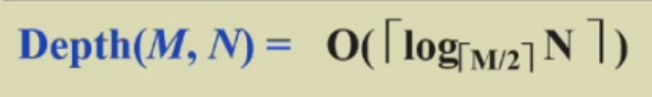
Lecture3 InvFileInd_Tch
1) 运用threshold的返回个数不确定,不可能得到top-k之类的

2) 常见的优化方向
Word Stemming: 有相同词干的词,比如 -ing/-ed/-ful/-ment 可以剪枝聚合成一个词。
Stop Word: 以英语为例,过于高频的词比如 and/the/a 对检索几乎没有帮助,不需要做索引。
Token Analyser: 很多语言,比如中文,并不便于分词断句,一个句子如何分词将直接影响到检索的效率。
Memory Management: 全球数据过于庞大,索引可以分批进行。由于已经被访问过的数据更新可能被访问原则,我们决定哪些数据留在内存中哪些放回硬盘时需要一定策略。
Auxiliary Index: 互联网上内容一直生产,索引需要及时更新。但是动态更新索引的 IO 开销很大。可以在内存中开辟一个小段辅助索引(auxiliary index)暂存新内容,然后大批量一次插入。
Distributed Index: 对于分布式服务器,你如何安置多台计算机存储数据使性能尽可能强且负载量均匀,以下是两种常用策略。
Solution 1: Term-partitioned index
Solution 2: Document-partitioned index
Compression: 索引压缩。对于一篇超长内容,想要从0开始计数某个单词出现的位置可能需要一个巨大的数字,这时可以对索引进行压缩

3) 两种方法进行单词检索:多叉树和哈希表
如下是多叉树,自上而下从根节点到叶子节点为一个单词
*
/ | \
a b c
/| | \
d e f g 哈希表
哈希表的缺点:哈希表是无序的,如果要按顺序查找单词,则会很困难
Index:
0: null
1: null
2: apple
3: null
4: banana
... 4) 长倒排表的词项通常是高频词

如果某个词的倒排表很长,意味着该词出现在了许多文档中。通常,这类词项是高频词或常见词,如 "the"、"is"、"and" 等。这些词对区分文档的相关性帮助不大,因为它们几乎在所有文档中都会出现。
Lecture4 LeftistSkew
1) 左式堆

自适应结构结果往往需要更多的操作
因为不需要维护平衡所以没有平衡信息,所占空间反而少了
2)⭐逐次插入节点 ‘1’,节点 ‘2’,不管谁先插入,最终结果都是这样的
2插入到1之后也要交换到左侧去,尽管原本1的左侧没有节点
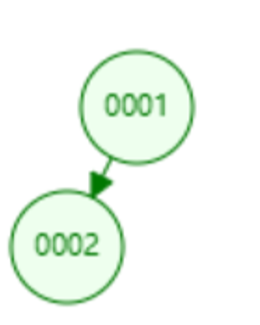
3) 最后一步插入的时候依然需要交换
⭐最后一步操作时,一个堆已经没有了,另一个堆还有若干节点且右路经长度为2;这时候插入的时候,13和14依然需要交换一次
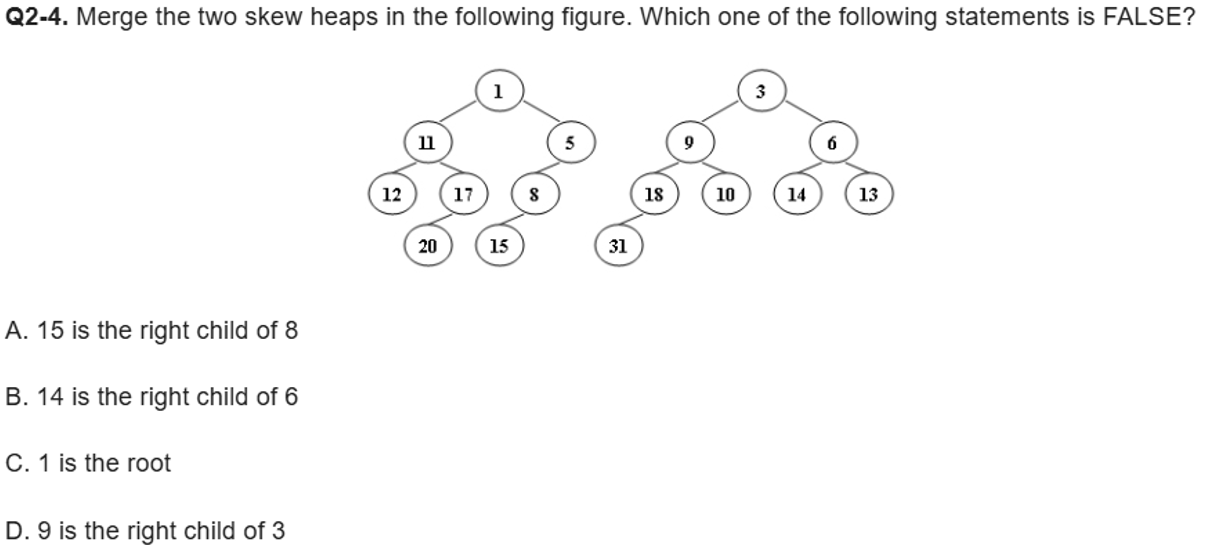
Lecture5 BinomialQ
1) ⭐二项堆的存储方式是 left-child-next-sibling (很容易在程序填空题中出现这样的问题)
2) ⭐根节点的子孩子按照从大到小的方式排列
3) 为什么要按size排列而不是堆顶元素大小排序?
优点:寻找最小值的时间为O(1)
缺点:
当我们需要执行大量的删除操作与少量的查找操作时;删除一次就要重新找最小值,十分费时-
合并二项堆操作需要按堆的高度排列
Lecture6 Backtracking
1) what vary?
What makes the time complexity analysis of a backtracking algorithm very difficult is that the number of solutions that do satisfy the restriction is hard to estimate.(True)
What makes the time complexity analysis of a backtracking algorithm very difficult is that the sizes of solution spaces may vary.(False)
2)α-β pruning 的时间复杂度是 O(bd/2)
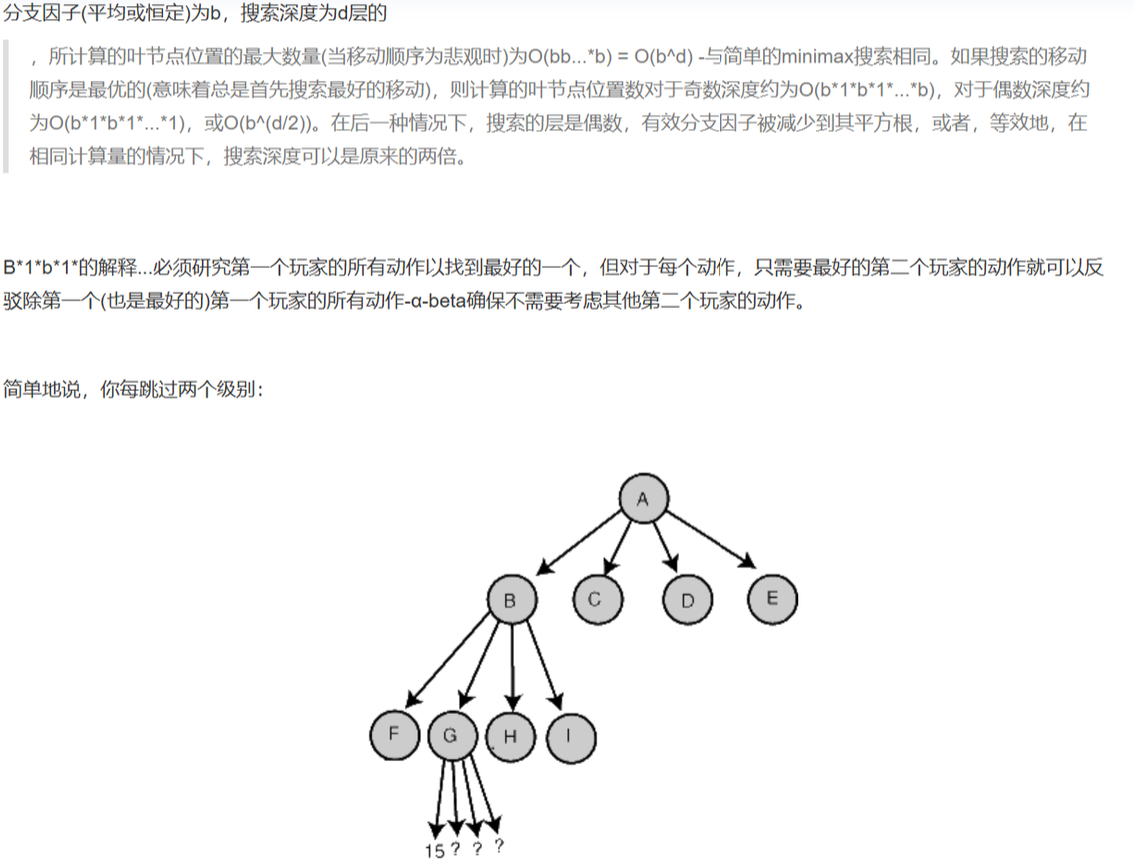
Lecture7 Divide Conquer
1) 利用还原法解决特殊等式

2) 🤔用换元法和substitution解决特殊等式
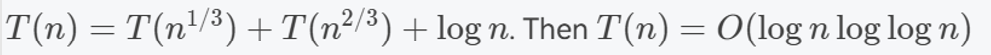
先换元,换元之后相当于要解决 T(N)=T(N/3)+T(2N/3)+cN 问题
然后利用substitution解决,设 对于子问题,T(N)=d*N*log(N) ,则 ,T(N)=T(N/3)+T(2N/3)+cN≤d(N/3)log(N/3)+d(2N/3)log(2N/3)+cN
=dNlogN−dN(log23/2)+cN≤dNlogN=dNlogN−dN(log23/2)+cN≤dNlogN (for some d′)
于是可以认为T(N)=d*N*log(N)
3)寻找平面最近点对问题
已知公式如下
关于为何across是O(N): 因为是先做divide再做conquer的,所以当做完两边的divide的时候,我们已经知道两边的最小距离δ了,接下来我们要寻找在跨越边界的区域是否存在更小的距离点对。那么在conquer过程中,取2δ作为搜寻范围(正方形)的边长,这个正方形被划分成两侧;(又由于条件,任意一侧的任意两点之间的距离不小于δ,所以任意一侧可搜寻的点是常数个的),所以搜寻的时间是常数时间的;对于n个点,搜寻时间就是 O(N).
一道题目
为何要按x,y坐标排序:因为要保证divide的时候是分成了N/2的大小,所以要找到中间分割点
Lecture8 Dynamic Programming
普通的矩阵乘法 时间复杂度是O(n3) , 空间复杂度是 O(n2)
Floyd-Warshall算法的 时间复杂度为 O(n3) 空间为O(n2) ⭐支持负边
这个算法的实现,是一共三层循环,待定中间节点放在第二层循环中 (考试大概率不考这么细节的。。)
Lecture9 Greedy
1) 最优解不一定是贪婪最优解
这句话错误的点在于, 在选择最大活动数量问题中,解空间会比贪婪最优解的数量多;例如,在空余时间区间[1,4],一个活动时间是
[1,3] 一个是 [2,4] ,这样我们选前者和后者都是解,但贪婪最优解只有一个,并不包括最早结束
2)在活动选择问题中,贪心算法时间复杂度是 O(NlogN),因为对活动排序花费了 O(N*logN)
3) 哈夫曼编码
(二叉树的)full binary tree 定义为每个节点要么是叶子要么是度为2
对于一些同样的待编码的字符,不同方式的哈夫曼编码,其树形态可能不一样,某些字符的编码长度可能不一样
为什么会出现这种情况呢?因为当恰有三个节点的出现频率相同时候,就有三种结合方式,不同的先后结合顺序是导致差异的关键
4) max activity-selection 拓展
如下的题目中,算法一错误,算法二正确
为什么第一个算法有误: 例如有可容纳[1,12]的容器,有一些占用空间的物品,占用空间分别为 [1,5],[6,7],[8,12],[1,3],[4,9],[10,12]
最优解是使用两个容器: ① [1,5],[6,7],[8,12] ② [1,3],[4,9],[10,12]
如果使用算法Ⅰ,就会得到: ① [1,3],[6,7],[10,12] ② [1,5],[8,12] ③ [4,9]
5) A Huffman tree with 61 nodes is the optimal coding tree for n characters. What a conclusion can we make for n?
最优编码树得是完全二叉树,所以n取31
Lecture10 NP-problem
1) 某些NPH问题没法用图灵机解决

2) 证明 Vertex Cover Problem 是 NPC 问题

方法:通过 Clique Problem(已知的NPC问题)的归约,来证明定点覆盖问题是 NPC 的
① 证明 Vertex Cover Problem 是多项式时间内可以被验证的,这是可以做到的 (O(N3)或O(N2)),这说明定点覆盖问题是NP的
② 进行规约,来证明其比NPC问题更难,规约方式如下:
给定一个图 G 和一个整数 K,我们想知道是否存在一个大小为 K 的团。
我们可以构造一个新的图 G(即图 G 的补图),并且证明:图 G 中存在一个大小为 K 的团,当且仅当图 G 中存在一个大小为 ∣V∣−K 的顶点覆盖。( 如果把这个证明的话,就可以通过寻找∣V∣−K 的顶点覆盖问题,来解决团问题,这说明了定点覆盖问题比团问题不严格地来说更难,于是团问题就可以归约到定点覆盖问题了 ) 证明如下:

因此,定点覆盖问题是NPC的
3) 如果 NP=P ,那么 NPC=NP=P
4) formal language theory

5) NP 和 co-NP 的几种可能的 关系
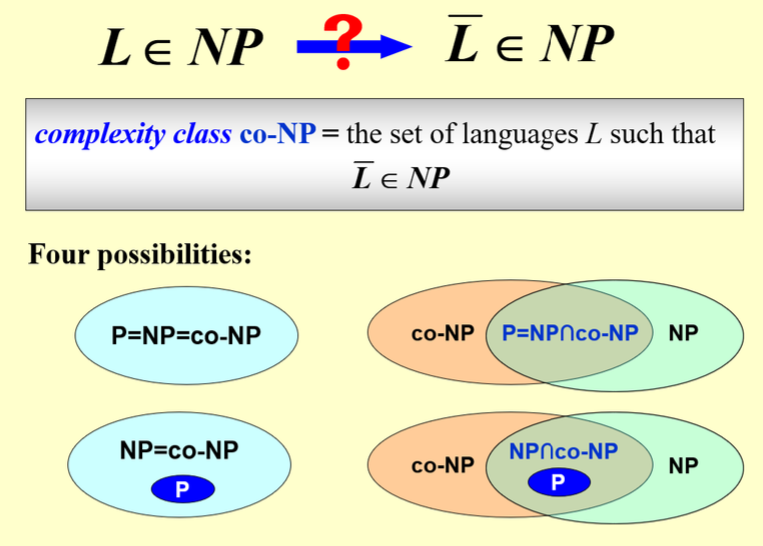
6)在这里规约的条件是 if and only if
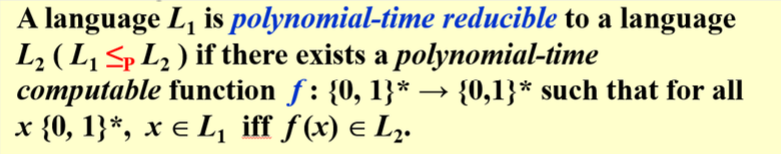
7) Given a weighted directed acyclic graph (DAG) G and a source vertex s in G, it is NP to find the longest distances from s to all other vertices in G.
可以使用动态规划或拓扑排序的方法在多项式时间内解决这个问题
8) 非确定性图灵机不是随机的,而是最lucky的
9) A 能规约到 B 并不是说 B 严格地比 A 难;有可能可以互相规约
Lecture11 Approximation
1) 定点覆盖问题有2-approximation的近似算法,团问题可以多项式地规约到定点覆盖问题,但这并不能推出团问题有2-approximation近似算法的结论
2)Even if P=NP, still we cannot guarantee Optimality Efficiency & All instances
3)If we delete an item from the input, is it guaranteed that the result of FF will no increase? No

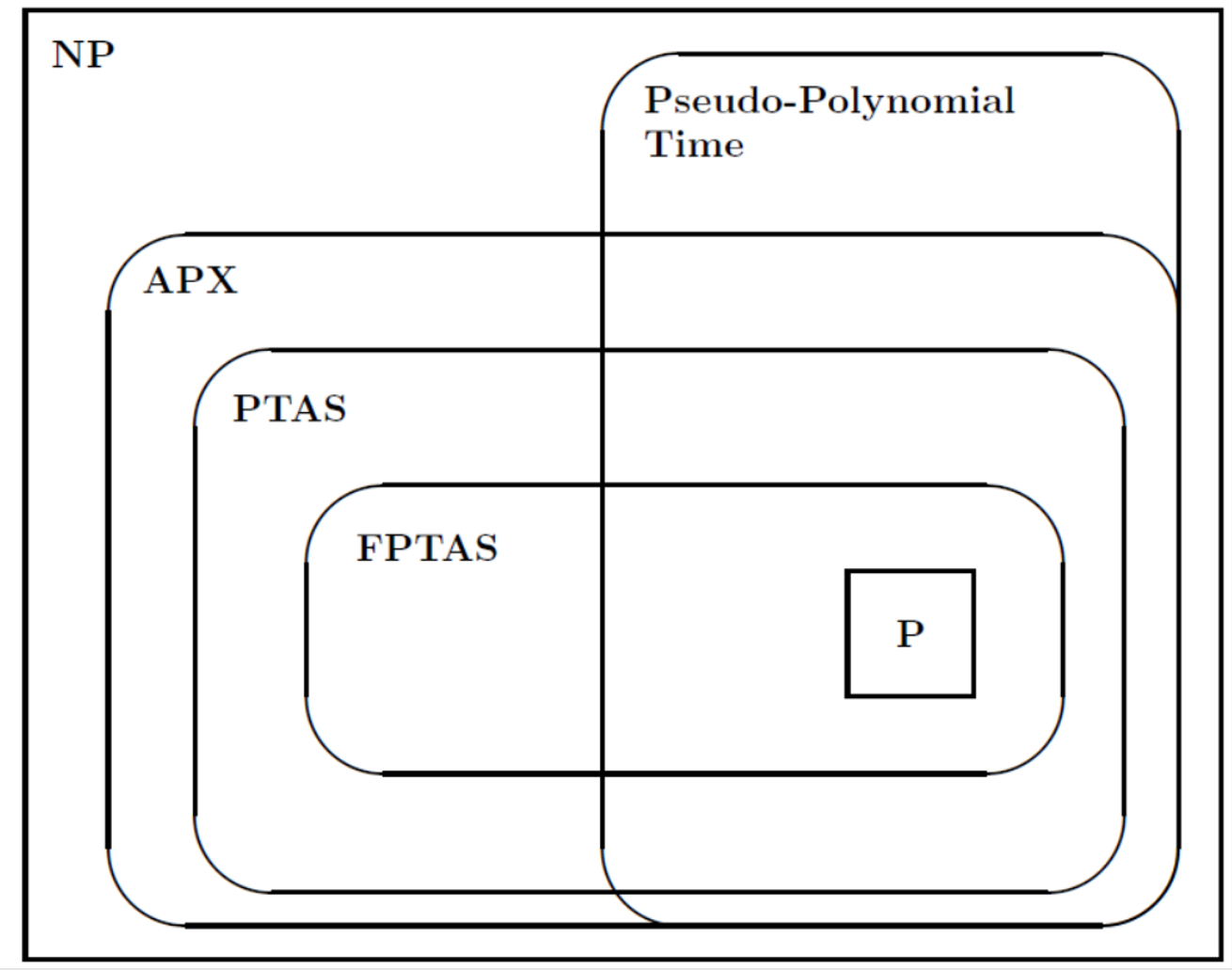
4) 关于 PTAS 和 FPTAS
5) 这句话错在:近似算法的近似界可能不是常数,而是一个(eg.)类似于 1/α 的东西,其中 α 趋近∞
6) Unless P = NP, there is no 𝜌 approximation for center selection problem for any 𝜌 < 2. PPT 上 𝜌=2
7) 存在某些输入数据,能够迫使任何在线装箱算法使用的箱子数量,至少 是最优装箱算法所需箱子数量的5/3倍。
8) 你需要在 20 个相同的核心上调度一些任务。每个任务 j∈{1,2,...,n} 有一个处理时间 pj>0。如果 Si 是分配给核心 i 的任务集合,目标是最小化所有核心中最大的负载值。为了实现这个目标,可以采用以下策略:每当一个新任务到达时,将其分配给当前负载最小的核心。这种方法的近似比为 1.95(更普遍的近似比表达式:2 - 1/n)。
考虑 这些任务 : 一个 大小为 20 , 19 * 20/𝜀个 𝜀 大小的,小任务先将每个core占用了19单位,大小为20 的最后放 ,其中一个core需要39单位;而在先放大任务,的状况下每个core只需要20个单位,39/20=1.95
9)为什么装箱问题的 next fit 方法是 2 近似比?
对于以下的装箱顺序,只需要4个箱子
(0.6 0.4) (0.59 0.41) (0.58 0.42) (0.57 0.43)而对于这样的顺序,则需要个7箱子
(0.58) (0.43) (0.59) (0.42) (0.6) (0.41) (0.4,0.57)
以上序列按大小来排序的话,公差为0.1,如果将这个公差进一步缩小,则可以得到更多的序列个数,由此得到2近似比的结论
Lecture12 Local Search
1)N皇后的local search 时间花费 O(N2)
如下的判断题是错误的,N皇后的 search space 是仅改变一个棋子的布尔值,一共有N2 种可能
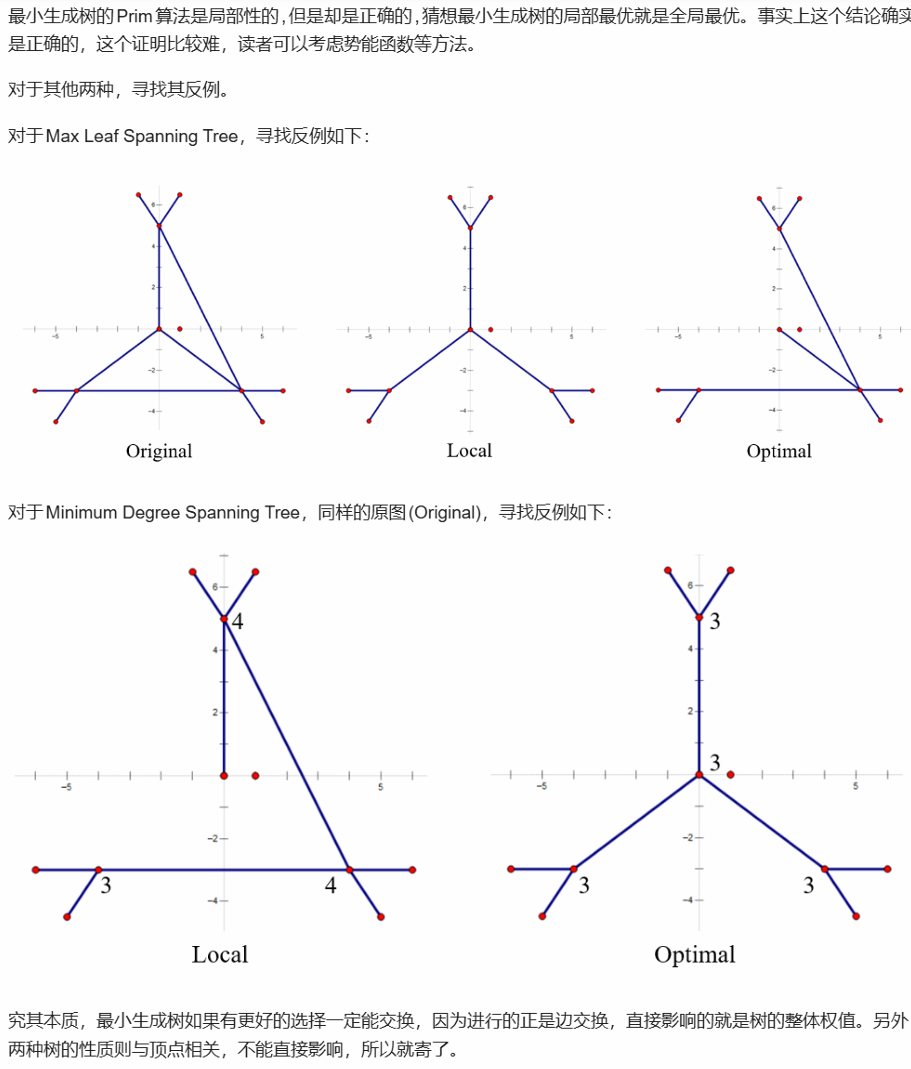
2)局部搜索算法在寻找最小边权生成树是全局最优的
来看以下这道题目,答案选B
接下来引用Jianjun Zhou学长的解析,能直接给出A、C的反例
实际上B的贪心算法与Kruskal算法的逻辑一致,最终必收敛到全局最优解
3)容易忽略的考点,big improvement flip (实际上2024年秋冬的卷子没考到任何有关近似比等需要记忆的考点,但以前考过)
4)如果一个划分(A,B)在p-flip规则下是局部最优的,那么对于所有k < p,它在k-flip规则下也是局部最优的
假设 (A,B) 是 p-flip规则下的局部最优,即所有移动 最多 p 个节点 的操作均无法改进解 ,显然对于所有k<p,k-flip下也无法改进解
5) 一道有关算法的题目
1,2,4 是正确的,我们武断地得出结论:在局部算法种,当一个任务l从a移动到b之后,那么就不可能再从b移动到a了(具体证明暂时没有想出来,如果你想出来了欢迎联系我!);因此一个任务最多被移动n次,n个任务最多被移动n2 次; 选项3应当是1.9 OPT,之前的章节笔记种已经提及过这是 2- 1/n 的近似比
Lecture13 Random Access
1) skip list (project 里的内容,做到过一道有关的题目,可以了解一下 Skip List--跳表(全网最详细的跳表文章没有之一) - 简书

插入删除查找平均时间都是 log(N)
2) 改进的快速排序算法能保证最差时间复杂度为 O(N*logN)
① 用中心分割点将问题分成两部分,每次选定的pivot保证了每个子问题的大小不会小于i/4(i是当前问题的大小)
② 我们要对这些子问题进行划分,于是,定义我们一个问题是type-j的,如果说这个问题的大小在 (N*(3/4)j+1, N*(3/4)j)范围内(N是最初问题的大小);
③ 我们不加证明的给出这样一个结论,对于任何一个type-j的问题,其元素个数不会超过 (4/3)j+1 个,因此,对于任何一个类型的问题,其总规模是O(N(3/4)j)*(4/3)j+1=O(N)的,而我们知道,对于任何一次快排,如果不考虑其子问题的话,就是相当于将所有数据和某个pivot比较了一遍,因此,其时间复杂度等价于其元素的个数;因此,对于任何type的数据,因为其总规模是O(N)的,所以我们需要花费的时间复杂度也是O(N);
④ 我们可以证明不同种类问题的数量是O(logN)级别的,因为type-(j+1)问题的大小是type-j 问题3/4 左右,因此问题的大小是指数级别减少的。
⑤ 综上所述,这种方法可以保证问题的最差的解决时间也在 O(NlogN)约束中
3) 一道有关普通快排的问题
在快排中,两个数据能够被比较的充要条件,就是其中一个被选中为pivot,并且两个数据在同一个划分中(即在两个数据被比较之前的,divide过程中这两个数据没有被分开);题目中 的2/(j-i+1)的概率只有在数列呈递增的情况下才是成立的,具体证明我也不会捏~
4)一道快排和主定理结合的题目
QAQ~
递归的时间复杂度可以表示为T(n) = T(3n/4) + O(n),根据主定理,答案是O(N)
5) 有n个候选人,他们以随机的顺序到达,且每个候选人的表现都不同。算法是:先面试前k个候选人,但不雇佣他们。然后从第k+1个候选人开始,如果当前候选人比前k个中的所有人都好,就雇佣他。问题是要计算期望雇佣多少人。
首先我们要明确,在面试k个人之后,是否选择第k+i个人对第k+i之后的人的选择不会产生影响
对于每个后续候选人i,他需要比前k个候选人中的所有人更好。这等价于在前k个候选人和当前候选人i组成的k+1人中,i是最优者,概率为1/(k+1) 。
总共有n−k个后续候选人,故期望是 (n-k)/(k+1)
Lecture14 parallel algorithm
1)random access 算法很大可能可以使得W变成O(N) ,时间为O(1)
2) 一道parallel和分治结合的题目
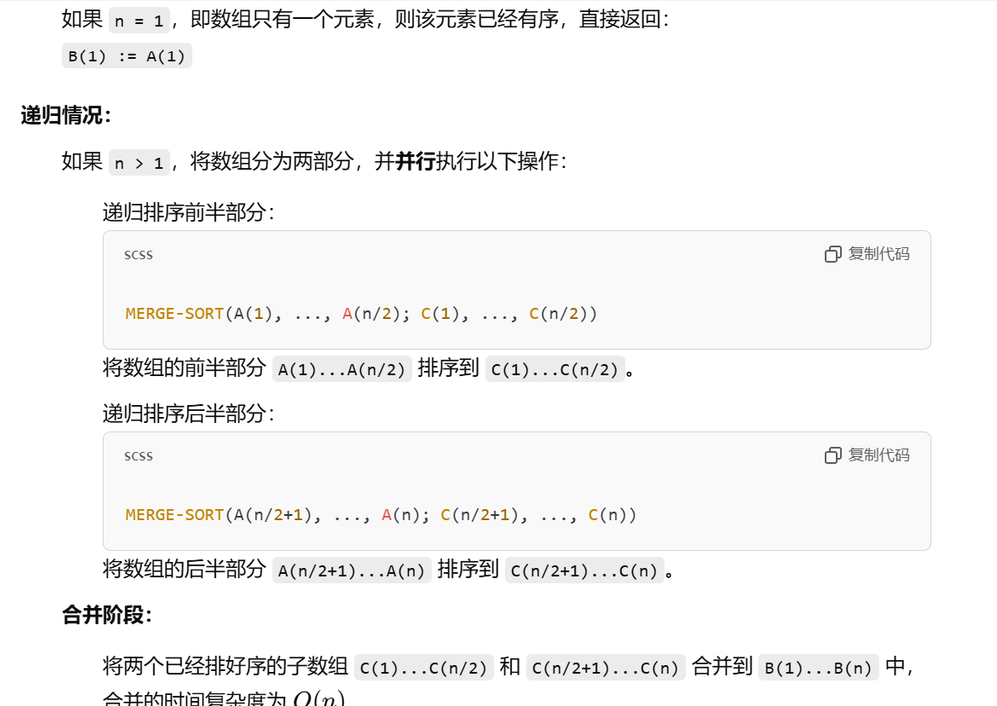
首先要明白题意是什么,用gpt表述了一下:
对于work的计算,通过公式W(N)=2W(N/2)+O(N),结合主定理,可以得出N*logN的结论
对于time的计算,T(N)=T(N/2)+O(N),所以我合理怀疑这道题T(N)=O(n),但答案给的是O(log2(N))
3) CRCW概念题
原本在可以同时读写的情况下,寻找最大值可以实现 W=O(N2) , T=O(1),关键在于维护一个大小为N的一维数组,原本全是1,一旦发现有任何数据别某个索引的数据大的时候,该一维数组对应的索引的数字变为0,这需要多个机器对某个索引有写入权。但如果的owner write的话,就只能有一个机器对某个索引的数据有写入权了。
4) 渐进等同
在并行算法中,我们经常使用工作负载 W(n)W(n) 和最坏情况运行时间 T(n)T(n) 来评估算法的性能。我们接下来的目标是找出这些评估指标在渐进行为上有多少种等价形式。
1,2 是正确的,这两个选项可以与 W(N)、T(N)相互转化
Lecture15 External Sort
看这位学长的 ==> Lec 15: External Sorting - NoughtQ的笔记本
1) ex1 (解析摘自jianjianzhou的笔记本)
2) ex2
3) ex3
由于有4个tapes,所以我们采取3-way merge (Fibonacci);我们先列出三阶斐波那契数列,即 1 ,1,1,3,5,9,17;然后我们去寻找 其中相邻的三个数,使得三个数之和大于等13(因为是13runs),并且要尽量小;于是我们锁定了3,5,9这三个数,3是第四个数,经过三次归并之后三个tape上分别有1段排序好的数据,最后将这三个tapes合并,也是一次归并;于是总共有四次归并